3.3: Categorization and Distributed Representations
- Page ID
- 12575

As explained in the introduction to this chapter, the process of forming categorical representations of inputs coming into a network enables the system to behave in a much more powerful and "intelligent" fashion (Figure 3.7). Philosophically, it is an interesting question as to where our mental categories come from -- is there something objectively real underlying our mental categories, or are they merely illusions we impose upon reality? Does the notion of a "chair" really exist in the real world, or is it just something that our brains construct for us to enable us to get by (and rest our weary legs)? This issue has been contemplated since the dawn of philosophy, e.g., by Plato with his notion that we live in a cave perceiving only shadows on the wall of the true reality beyond the cave. It seems plausible that there is something "objective" about chairs that enables us to categorize them as such (i.e., they are not purely a collective hallucination), but providing a rigorous, exact definition thereof seems to be a remarkably challenging endeavor (try it! don't forget the cardboard box, or the lump of snow, or the miniature chair in a dollhouse, or the one in the museum that nobody ever sat on..). It doesn't seem like most of our concepts are likely to be true "natural kinds" that have a very precise basis in nature. Things like Newton's laws of physics, which would seem to have a strong objective basis, are probably dwarfed by everyday things like chairs that are not nearly so well defined (and "naive" understanding of physics is often not actually correct in many cases either).
The messy ontological status of conceptual categories doesn't bother us very much. As we saw in the previous chapter, Neurons are very capable detectors that can integrate many thousands of different input signals, and can thereby deal with complex and amorphous categories. Furthermore, we will see that learning can shape these category representations to pick up on things that are behaviorally relevant, without requiring any formality or rigor in defining what these things might be. In short, our mental categories develop because they are useful to us in some way or another, and the outside world produces enough reliable signals for our detectors to pick up on these things. Importantly, a major driver for learning these categories is social and linguistic interaction, which enables very complex and obscure things to be learned and shared -- the strangest things can be learned through social interactions (e.g., you now know that the considerable extra space in a bag of chips is called the "snackmosphere", courtesy of Rich Hall). Thus, our cultural milieu plays a critical role in shaping our mental representations, and is clearly a major force in what enables us to be as intelligent as we are (we do occasionally pick up some useful ideas along with things like "snackmosphere"). If you want to dive deeper into the philosophical issues of truth and relativism that arise from this lax perspective on mental categories, see Philosophy of Categories.
One intuitive way of understanding the importance of having the right categories (and choosing them appropriately for the given situation) comes from insight problems. These problems are often designed so that our normal default way of categorizing the situation leads us in the wrong direction, and it is necessary to re-represent the problem in a new way ("thinking outside the box"), to solve it. For example, consider this "conundrum" problem: "two men are dead in a cabin in the woods. what happened?" -- you then proceed to ask a bunch of true/false questions and eventually realize that you need to select a different way of categorizing the word "cabin" in order to solve the puzzle. Here is a list of some of these kinds of conundrums: http://www.angelfire.com/oh/abnorm/ (WARNING: click at own risk for external links -- seems ok but does pop up an ad or two it seems).
For computer programmers, one of the most important lessons one learns is that choosing the correct representation is the most important step in solving a given problem. As a simple example, using the notion of a "heap" enables a particularly elegant solution to the sorting problem. Binary trees are also a widely used form of representation that often greatly reduce the computational time of various problems. In general, you simply want to find a representation that makes it easy to do the things you need to do. This is exactly what the brain does.
One prevalent example of the brain's propensity to develop categorical encodings of things are stereotypes. A stereotype is really just a mental category applied to a group of people. The fact that everyone seems to have them is strong evidence that this is fundamentally how the brain works. We cannot help but think in terms of abstract categories like this, and as we've argued above, categories in general are essential for allowing us to deal with the world in an intelligent manner. But the obvious problems with stereotypical thinking also indicate that these categories can also be problematic (for stereotypes specifically and categorical thinking more generally), and limit our ability to accurately represent the details of any given individual or situation. As we discuss next, having many different categorical representations active at the same time can potentially help mitigate these problems. The ability to entertain multiple such potential categories at the same time may be an individual difference variable associated with things like political and religious beliefs (todo: find citations). This stuff can get interesting!
Distributed Representations
In addition to our mental categories being somewhat amorphous, they are also highly polymorphous: any given input can be categorized in many different ways at the same time -- there is no such thing as the appropriate level of categorization for any given thing. A chair can also be furniture, art, trash, firewood, doorstopper, plastic and any number of other such things. Both the amorphous and polymorphous nature of categories are nicely accommodated by the notion of a distributed representation. Distributed representations are made up of many individual neurons-as-detectors, each of which is detecting something different. The aggregate pattern of output activity ("detection alarms") across this population of detectors can capture the amorphousness of a mental category, because it isn't just one single discrete factor that goes into it. There are many factors, each of which plays a role. Chairs have seating surfaces, and sometimes have a backrest, and typically have a chair-like shape, but their shapes can also be highly variable and strange. They are often made of wood or plastic or metal, but can also be made of cardboard or even glass. All of these different factors can be captured by the whole population of neurons firing away to encode these and many other features (e.g., including surrounding context, history of actions and activities involving the object in question).
The same goes for the polymorphous nature of categories. One set of neurons may be detecting chair-like aspects of a chair, while others are activating based on all the different things that it might represent (material, broader categories, appearance, style etc). All of these different possible meanings of the chair input can be active simultaneously, which is well captured by a distributed representation with neurons detecting all these different categories at the same time.


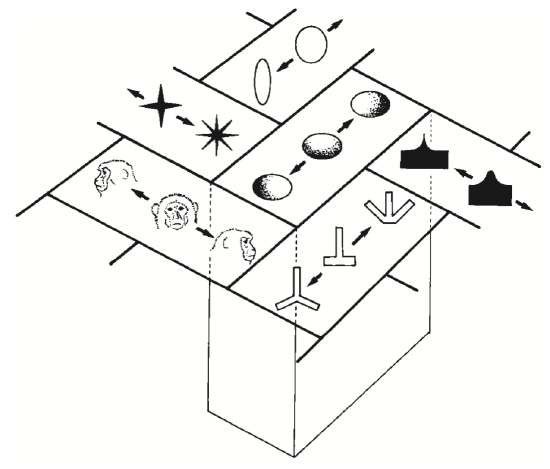
Some real-world data on distributed representations is shown in Figure 3.8 and Figure 3.9. These show that individual neurons respond in a graded fashion as a function of similarity to inputs relative to the optimal thing that activates them (we saw this same property in the detector exploration from the Neuron Chapter, when we lowered the leak level so that it would respond to multiple inputs). Figure 3.10 shows an overall summary map of the topology of shape representations in monkey inferotemporal (IT) cortex, where each area has a given optimal stimulus that activates it, while neighboring areas have similar but distinct such optimal stimuli. Thus, any given shape input will be encoded as a distributed pattern across all of these areas to the extent that it has features that are sufficiently similar to activate the different detectors.
Another demonstration of distributed representations comes from a landmark study by Haxby and colleagues (2001), using functional magnetic resonance imaging (fMRI) of the human brain, while viewing different visual stimuli (Figure 3.11). They showed that contrary to prior claims that the visual system was organized in a strictly modular fashion, with completely distinct areas for faces vs. other visual categories, for example, there is in fact a high level of overlap in activation over a wide region of the visual system for these different visual inputs. They showed that you can distinguish which object is being viewed by the person in the fMRI machine based on these distributed activity patterns, at a high level of accuracy. Critically, this accuracy level does not go down appreciably when you exclude the area that exhibits the maximal response for that object. Prior "modularist" studies had only reported the existence of these maximally responding areas. But as we know from the monkey data, neurons will respond in a graded way even if the stimulus is not a perfect fit to their maximally activating input, and Haxby et al. showed that these graded responses convey a lot of information about the nature of the input stimulus.

See More Distributed Representations Examples for more interesting empirical data on distributed representations in the cortex.
Coarse Coding
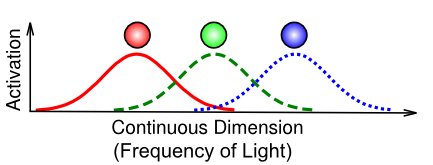
Figure 3.12 illustrates an important specific case of a distributed representation known as coarse coding. This is not actually different from what we've described above, but the particular example of how the eye uses only 3 photoreceptors to capture the entire visible spectrum of light is a particularly good example of the power of distributed representations. Each individual frequency of light is uniquely encoded in terms of the relative balance of graded activity across the different detectors. For example, a color between red and green (e.g., a particular shade of yellow) is encoded as partial activity of the red and green units, with the relative strength of red vs. green determining how much it looks more orange vs. chartreuse. In summary, coarse coding is very important for efficiently encoding information using relatively few neurons.
Localist Representations
The opposite of a distributed representation is a localist representation, where a single neuron is active to encode a given category of information. Although we do not think that localist representations are characteristic of the actual brain, they are nevertheless quite convenient to use for computational models, especially for input and output patterns to present to a network. It is often quite difficult to construct a suitable distributed pattern of activity to realistically capture the similarities between different inputs, so we often resort to a localist input pattern with a single input neuron active for each different type of input, and just let the network develop its own distributed representations from there.

Figure 3.13 shows the famous case of a "Halle Berry" neuron, recorded from a person with epilepsy who had electrodes implanted in their brain. This would appear to be evidence for an extreme form of localist representation, known as a grandmother cell (a term apparently coined by Jerry Lettvin in 1969), denoting a neuron so specific yet abstract that it only responds to one's grandmother, based on any kind of input, but not to any other people or things. People had long scoffed at the notion of such grandmother cells. Even though the evidence for them is fascinating (including also other neurons for Bill Clinton and Jennifer Aniston), it does little to change our basic understanding of how the vast majority of neurons in the cortex respond. Clearly, when an image of Halle Berry is viewed, a huge number of neurons at all levels of the cortex will respond, so the overall representation is still highly distributed. But it does appear that, amongst all the different ways of categorizing such inputs, there are a few highly selective "grandmother" neurons! One other outstanding question is the extent to which these neurons actually do show graded responses to other inputs -- there is some indication of this in the figure, and more data would be required to really test this more extensively.
Explorations
See Face Categorization (Part I only) for an exploration of how face images can be categorized in different ways (emotion, gender, identity), each of which emphasizes some aspect of the input stimuli and collapses across others.