3.5: Inhibitory Competition and Activity Regulation
- Page ID
- 12577
Inhibitory competition plays a critical role in enabling us to focus on a few things at a time, which we can then process effectively without getting overloaded. Inhibition also ensures that those detectors that do get activated are the ones that are the most excited by a given input -- in Darwinian evolutionary terms, these are the fittest detectors.
Without inhibition, the bidirectional excitatory connectivity in the cortex would quickly cause every neuron to become highly excited, because there would be nothing to check the spread of activation. There are so many excitatory connections among neurons that it doesn't take long for every neuron to become activated. A good analogy is placing a microphone near a speaker that is playing the sound from that microphone -- this is a bidirectional excitatory system, and it quickly leads to that familiar, very loud "feedback" squeal. If one's audio system had the equivalent of the inhibitory system in the cortex, it would actually be able to prevent this feedback by dynamically turning down the input gain on the microphone, and/or the output volume of the speaker.
Another helpful analogy is to an air conditioner (AC), which has a thermostat control that determines when it kicks in (and potentially how strong it is). This kind of feedback control system allows the room to warm up to a given set point (e.g., 75 degrees F) before it starts to counter the heat. Similarly, inhibition in the cortex is proportional to the amount of excitation, and it produces a similar set point behavior, where activity is prevented from getting too high: typically no more than roughly 15-25% of neurons in any given area are active at a time.
The importance of inhibition goes well beyond this basic regulatory function, however. Inhibition gives rise to competition -- only the most strongly excited neurons are capable of overcoming the inhibitory feedback signal to get activated and send action potentials to other neurons. This competitive dynamic has numerous benefits in processing and learning. For example, selective attention depends critically on inhibitory competition. In the visual domain, selective attention is evident when searching for a stimulus in a crowded scene (e.g., searching for a friend in a crowd as described in the introduction). You cannot process all of the people in the crowd at once, so only a relatively few capture your attention, while the rest are ignored. In neural terms, we say that the detectors for the attended few were sufficiently excited to out-compete all the others, which remain below the firing threshold due to the high levels of inhibition. Both bottom-up and top-down factors can contribute to which neural detectors get over threshold or not, but without inhibition, there wouldn't be any ability to select only a few to focus on in the first place. Interestingly, people with Balint's syndrome, who have bilateral damage to the parietal cortex (which plays a critical role in spatial attention of this sort), show reduced attentional effects and also are typically unable to process anything if a visual display contains more than one item (i.e., "simultanagnosia" -- the inability to recognize objects when there are multiple simultaneously present in a scene). We will explore these phenomena in the Perception Chapter.
We will see in the Learning Chapter that inhibitory competition facilitates learning by providing this selection pressure, whereby only the most excited detectors get activated, which then gets reinforced through the learning process to make the most active detectors even better tuned for the current inputs, and thus more likely to respond to them again in the future. This kind of positive feedback loop over episodes of learning leads to the development of very good detectors for the kinds of things that tend to arise in the environment. Without the inhibitory competition, a large percentage of neurons would get trained up for each input, and there would be no specialization of detectors for specific categories in the environment. Every neuron would end up weakly detecting everything, and thus accomplish nothing. Thus, again we see that competition and limitations can actually be extremely beneficial.
A summary term for the kinds of neural patterns of activity that develop in the presence of inhibitory competition is sparse distributed representations. These have relatively few (15-25%) neurons active at a time, and thus these neurons are more highly tuned for the current inputs than they would otherwise be in a fully distributed representation with much higher levels of overall activity. Thus, although technically inhibition does not contribute directly to the basic information processing functions like categorization, because inhibitory connectivity is strictly local within a given cortical area, inhibition does play a critical indirect role in shaping neural activity patterns at each level.
Feedforward and Feedback Inhibition
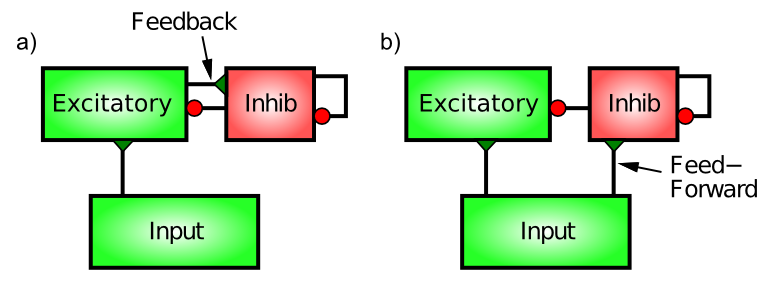
There are two distinct patterns of neural connectivity that drive inhibitory interneurons in the cortex, feedforward and feedback (Figure 3.16). Just to keep things interesting, these are not the same as the connections among excitatory neurons. Functionally, feedforward inhibition can anticipate how excited the excitatory neurons will become, whereas feedback accurately reflects the actual level of activation they achieve.
Feedback inhibition is the most intuitive, so we'll start with it. Here, the inhibitory interneurons are driven by the same excitatory neurons that they then project back to and inhibit. This is the classical "feedback" circuit from the AC example. When a set of excitatory neurons starts to get active, they then communicate this activation to the inhibitory interneurons (via excitatory glutamatergic synapses onto inhibitory interneurons -- inhibitory neurons have to get excited just like everyone else). This excitation of the inhibitory neurons then causes them to fire action potentials that come right back to the excitatory neurons, opening up their inhibitory ion channels via GABA release. The influx of Cl- (chloride) ions from the inhibitory input channels on these excitatory neurons acts to drive them back down in the direction of the inhibitory driving potential (in the tug-of-war analogy, the inhibitory guy gets bigger and pulls harder). Thus, excitation begets inhibition which counteracts the excitation and keeps everything under control, just like a blast of cold air from the AC unit.
Feedforward inhibition is perhaps a bit more subtle. It operates when the excitatory synaptic inputs to excitatory neurons in a given area also drive the inhibitory interneurons in that area, causing the interneurons to inhibit the excitatory neurons in proportion to the amount of excitatory input they are currently receiving. This would be like a thermostat reacting to the anticipated amount of heat, for example, by turning on the AC based on the outside temperature. Thus, the key difference between feedforward and feedback inhibition is that feedforward reflects the net excitatory input, whereas feedback reflects the actual activation output of a given set of excitatory neurons.
As we will see in the exploration, the anticipatory function of feedforward inhibition is crucial for limiting the kinds of dramatic feedback oscillations that can develop in a purely feedback-driven system. However, too much feedforward inhibition makes the system very slow to respond, so there is an optimal balance of the two types that results in a very robust inhibitory dynamic.
Exploration of Inhibitory Interneuron Dynamics
- Inhibition (inhib.proj) -- this simulation shows how feedforward and feedback inhibitory dynamics lead to the robust control of excitatory pyramidal neurons, even in the presence of bidirectional excitation.
FFFB Inhibition Function
We can efficiently implement the feedforward (FF) and feedback (FB) form of inhibition without actually requiring the inhibitory interneurons, by using the average net input and activity levels in a given layer, in a simple equation shown below. This works surprisingly well, without requiring subsequent parameter adaptation during learning, and this FFFB form of inhibition is now the default, replacing the k-Winners-Take-All (kWTA) form of inhibition used in the 1st Edition of the textbook.
The average excitatory net input to a layer (or group of units within a layer, if inhibition is operating at that level) is just the average of the net input (\(\eta_{i}\)) of each unit in the layer / group:
- \(<\eta>=\sum_{n} \frac{1}{n} \eta_{i}\)
Similarly, the average activation is just the average of the activation values (\(y_{i}\)):
- \(<y>=\sum_{n} \frac{1}{n} y_{i}\)
We compute the overall inhibitory conductance applied uniformly to all the units in the layer / group with just a few key parameters applied to each of these two averages. Because the feedback component tends to drive oscillations (alternately over and under reacting to the average activation), we apply a simple time integration dynamic on that term. The feedforward does not require this time integration, but it does require an offset term, which was determined by fitting the actual inhibition generated by our earlier kWTA equations. Thus, the overall inhibitory conductance is just the sum of the two terms (ff and fb), with an overall inhibitory gain factor gi:
- \(g_{i}(t)=\operatorname{gi}[\mathrm{ff}(t)+\mathrm{fb}(t)]\)
This gi factor is typically the only parameter manipulated to determine how active overall a layer is. Typically a value of 1.5 is as low as is used, to give a more widely distributed activation pattern, with values around 2.0 (often 2.1 or 2.2 works best) being very typical. For very sparse layers (e.g., a single output unit active), values up to around 3.5 or so can be used.
The feedforward (ff) term is:
- \(\mathrm{ff}(t)=\mathrm{ff}[<\eta>-\mathrm{ff} 0]_{+}\)
where ff is the overall gain factor for the feedforward component (set to 1.0 by default), and ff0 is an offset (set to 0.1 by default) that is subtracted from the average netinput value " src="https://grey.colorado.edu/mediawiki/...c90b756a54.png">.
The feedback (fb) term is:
- \(\mathrm{fb}(t)=\mathrm{fb}(t-1)+d t[\mathrm{fb}<y>-\mathrm{fb}(t-1)]\)
where fb is the overall gain factor for the feedback component (0.5 default), dt is the time constant for integrating the feedback inhibition (0.7 default), and the t-1 indicates the previous value of the feedback inhibition -- this equation specifies a graded folding-in of the new inhibition factor on top of what was there before, and the relatively fast dt value of 0.7 makes it track the new value fairly quickly -- there is just enough lag to iron out the oscillations.
Overall, it should be clear that this FFFB inhibition is extremely simple to compute (much simpler than the previous kWTA computation), and it behaves in a much more proportional manner relative to the excitatory drive on the units -- if there is higher overall excitatory input, then the average activation overall in the layer will be higher, and vice-versa. The previous kWTA-based computation tended to be more rigid and imposed a stronger set-point like behavior. The FFFB dynamics, being much more closely tied to the way inhibitory interneurons actually function, should provide a more biologically accurate simulation.
Exploration of FFFB Inhibition
To see FFFB inhibition in action, you can follow the instructions at the last part of the Inhibition (inhib.proj) model.