22.12A: Mechanisms of Chemical Digestion
- Page ID
- 8065
Chemical digestion is the enzyme-mediated, hydrolysis process that breaks down large macronutrients into smaller molecules.
- Differentiate among the methods used to chemically break down food molecules
Key Points
- Carbohydrates are mainly taken in the form of amylose and glycogen. Amylases hydrolyze the long carbohydrate chains that break amylose down into disaccharides, and glycogen into polysaccharides. The enzymes in the small intestine then break these down to monosaccharides.
- Proteins are digested by hydrolysis of the carbon–nitrogen (C–N) bond. Peptidases are secreted in an inactive form, to prevent auto-digestion. Endopeptidases cleave the polypeptides at the interior peptide bonds, and the exopeptidases cleave the terminal amino acids.
- Fats are digested by lipases that hydrolyze the glycerol fatty acid bonds. Bile salts emulsify the fats to allow for their solution as micelles in the chyme and to increase the surface area for the pancreatic lipases to operate.
- RNA and DNA are hydrolized by the pancreatic enzymes (ribonucleases, deoxyribonucleases) into nucleic acids, which are further broken down to purine and pyrimidine bases and pentoses, by enzymes in the intestinal mucosa (nucleases).
- Once the voluntary signal to defecate is sent back from the brain, the final phase begins.
Key Terms
- peptidase: Any enzyme that catalyzes the hydrolysis of peptides into amino acids; a protease.
- amylase: Any of a class of digestive enzymes that are present in saliva and that break down complex carbohydrates, such as starch, into simple sugars, such as glucose.
- hydrolysis: The degradation of certain biopolymers (proteins, complex sugars) by the chemical process that results in smaller polymers or monomers, such as amino acids or monosaccharides.
EXAMPLES
Because amylase turns some potato or rice starch into sugar, these foods taste slightly sweet.
Digestion is a form of catabolism: a breakdown of large food molecules (i.e., polysaccharides, proteins, fats, nucleic acids) into smaller ones (i.e., monosaccharides, amino acids, fatty acids, nucleotides).
Catabolism: A simplified outline of the catabolism of proteins, carbohydrates, and fats.
Carbohydrates are taken in mainly in the form of plant carbohydrate (amylose) and animal carbohydrate (glycogen) together with some sugars, mainly disaccharides. About 80% of the western diet is in the form of amylose. Amylose is not highly branched and consists mainly of long chains of glucose linked by α1:4 linkages.
Cellulose, the most abundant starch in nature, is formed of β1:4 linkages and cannot be digested in humans, although the bacterial action in the colon does break down a minute amount of it.
Glycogen is a multi-branched starch with linkages at the 1:4 and 1:6 position. This creates very large granules of multi-branched starch. Both the parotid and pancreatic amylases hydrolyse the 1:4 link, but not the terminal 1:4 links or the 1:6 links. This breaks amylose down into mainly disaccharides, and glycogen with its 1:6 linkages into polysaccharides.
The net result of these actions are numerous disaccharides and polysaccharides. Enzymes attached to the enterocycytes of the small intestine break these down to monosaccharides.
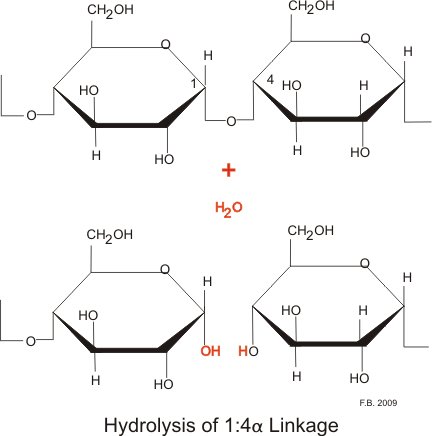
Hydrolysis by amylase: Both the parotid and pancreatic amylases hydrolyse the 1:4 link, but not the terminal 1:4 links or the 1:6 links.
Proteins and polypeptides are digested by hydrolysis of the carbon–nitrogen (C–N) bond. The proteolytic enzymes are all secreted in an inactive form, to prevent auto-digestion, and are activated in the lumen of the gut. Activation is caused by HCl in the case of the stomach enzyme pepsinogen, and by enteropeptidase and trypsin in the case of the pancreatic enzymes.
Final digestion takes place by small intestine enzymes that are embedded in the brush border of the small intestine. The enzymes are divided into endo- and exo-peptidases.
- The endopeptidases cleave the polypeptide at the interior peptide bonds, while the exopeptidases cleave the terminal amino acid.
- Exopeptidases are further subclassified into aminopeptidases—that cleave off the terminal amino acid at the amine end of the chain—and carboxypeptidases that cleave off the terminal amino acid at the carboxyl end of the chain.
Stomach pepsin cleaves the interior bonds of the amino acids, and is particularly important for its ability to digest collagen. This is a major constituent of the connective tissue of meat. In the absence of stomach pepsin, digestion in the small intestine proceeds with difficulty. Stomach pepsin digests about 20% of the proteins, and the rest are digested by the pancreatic and small intestine enzymes.
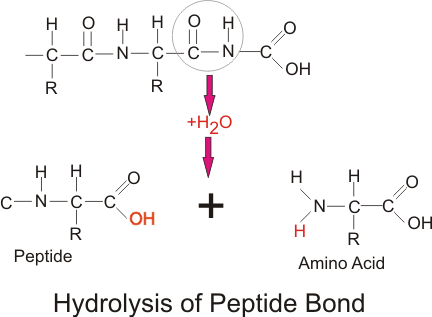
Hydrolysis of peptide bond: Proteins and polypeptides are digested by hydrolysis of the C–N bond.
Fats are digested by lipases that hydrolyze the glycerol fatty acid bonds. Of particular importance in fat digestion and absorption are the bile salts, which emulsify the fats to allow for their solution as micelles in the chyme, and increase the surface area for the pancreatic lipases to operate.
Lipases are found in the mouth, the stomach, and the pancreas. Because the lingual lipase is inactivated by stomach acid, it is formally believed to be mainly present for oral hygiene and for its anti-bacterial effect in the mouth. However, it can continue to operate on food stored in the fundus of the stomach, and as much as 30% of the fats can be digested by this lipase.
Gastric lipase is of little importance in humans. Pancreatic lipase accounts for the majority of fat digestion and operates in conjunction with the bile salts.
RNA and DNA are hydrolized by the pancreatic enzymes (ribonucleases, deoxyribonucleases) into nucleic acids, which are further broken down to purine and pyrimidine bases and pentoses, by enzymes in the intestinal mucosa (nucleases).

