21.2: Basics of statistical inference
- Page ID
- 13729
2.1 Types of outcome measure
The appropriate method of statistical analysis depends on the type of outcome measure that is of interest. An outcome in an intervention study can usually be expressed as a proportion, rate, or mean. For example, in a trial of a modified vaccine, an outcome measure of interest may be the proportion of vaccinated subjects who develop a protective level of antibodies. In a trial of multi-drug therapy for tuberculosis, the incidencerates of relapse, following treatment, may be compared in the different study groups under consideration. In a trial of an anti-malarial intervention, it may be of interest to compare the mean packed cell volume (PCV) at the end of the malaria season in those in the intervention group and those in the comparison group.
2.2 Confidence intervals
An estimate of an outcome measure calculated in an intervention study is subject to sampling error, because it is based on only a sample of individuals and not on the whole population of interest. The term sampling error does not mean that the sampling procedure or method of randomization was applied incorrectly, but that, when random sampling is used to decide which individuals are in which group, there will be an element of random variation in the results. The methods of statistical inference allow the investigator to draw conclusions about the true value of the outcome measure on the basis of the information in the sample. In general, the observed value of the outcome measure gives the best estimate of the true value. In addition, it is useful to have some indication of the precision of this estimate, and this is done by calculating a confidence interval for the estimate. The CI is a range of plausible values for the true value of the outcome measure, based on the observations in the trial. It is conventional to quote the 95% confidence interval (also called 95% confidence limits). This is calculated in such a way that there is a 95% probability that the CI includes the true value of the outcome measure.
Suppose the true value of the outcome measure is ø and that this is estimated from the sample data as øˆ . The 95% CIs to be presented here are generally of the form \(\hat{ø}±1.96×SE(\hat{ø})\), where \(SE (\hat{ø})\) denotes the standard error of the estimate. This is a measure of the amount of sampling error to which the estimate is susceptible. One of the factors influencing the magnitude of the standard error, and hence the width of the CI,
is the sample size; the larger the sample, the narrower the CI.
The multiplying factor 1.96, used when calculating the 95% CI, is derived from tables
of the Normal distribution. In this distribution, 95% of values are expected to fall within 1.96 standard deviations of the mean. In some circumstances, CIs, other than 95% limits, may be required, and then different values of the multiplying factor are appropriate, as indicated in Table 21.1.
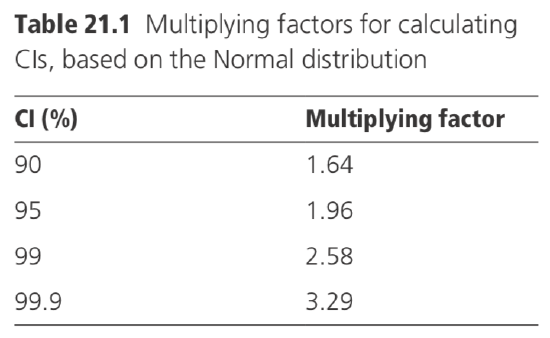
When analysing means, the multiplying factor sometimes has to be increased to allow for additional errors in estimating the standard error (see Section 5).
2.3 Statistical tests
As well as calculating a CI to indicate a range of plausible values for the outcome measure of interest, it may be appropriate to test a specific hypothesis about the outcome measure. In the context of an intervention trial, this will often be the hypothesis that there is no true difference between the outcomes in the groups under comparison. (For this reason, the hypothesis is often referred to as the null hypothesis.) The objective is thus to assess whether any observed difference in outcomes between the study groups may have occurred just by chance, due to sampling error.
A statistical test is used to evaluate the plausibility of the null hypothesis. The sample data are used to calculate a quantity (called a statistic) which gives a measure of the difference between the groups, with respect to the outcome(s) of interest. The details of how the statistic is calculated vary, according to the type of outcome measure being examined, and are given in Sections 4 to 6. Once the statistic has been calculated, its value is referred to an appropriate set of statistical tables, in order to determine the p-value (probability value) or statistical significance of the results. The p-value measures the probability of obtaining a value for the statistic as extreme as the one actually observed if the null hypothesis were true. Thus, a very low p-value indicates that the null hypothesis is likely to be false.
For example, suppose, in a trial of a vaccine against malaria, an estimate of the efficacy is obtained of 20%, with an associated p-value of 0.03. This indicates that, if the vaccine had a true efficacy of zero, there would only be a 3% chance of obtaining an observed efficacy of 20% or greater.
The smaller the p-value, the less plausible the null hypothesis is as an explanation of the observed data. For example, on the one hand, a p-value of 0.001 implies that the null hypothesis is highly implausible, and this can be interpreted as very strong evidence of a real difference between the groups. On the other hand, a p-value of 0.20 implies that a difference of the observed magnitude could quite easily have occurred by chance, even if there were no real difference between the groups. Conventionally, p-values of 0.05 and below have been regarded as sufficiently low to be taken as reasonable evidence against the null hypothesis and have been referred to as indicating a statistically significant difference, but it is preferable to specify the actual size of the p-value attained, so that readers can draw their own conclusions about the strength of the evidence.
While a small p-value can be interpreted as evidence for a real difference between the groups, a larger non-significant p-value must not be interpreted as indicating that there is no difference. It merely indicates that there is insufficient evidence to reject the null hypothesis, so that there may be no true difference between the groups. It is never possible to prove the null hypothesis. Depending on the size of the study and the observed difference between the groups under comparison, the CI on the difference provides a range of plausible values in which the true difference might lie, which may include a zero difference.
Too much reliance should not be placed on the use of statistical tests. Usually, it is more important to estimate the effect of the intervention and to specify a CI around the estimate to indicate the plausible range of effect than it is to test a specific hypothesis. In any case, a null hypothesis of zero difference is often of no practical interest, as there may be strong grounds for believing the intervention has some effect, and the main objective should be to estimate that effect.
The statistical tests presented here are two-sided tests. This means that, when the p-value is computed, it measures the probability (if the null hypothesis is true) of observing a difference as great as that actually observed in either direction (i.e. positive or negative). It is usual to assume that tests are two-sided, unless otherwise stated, though not all authors adhere to this convention. A full discussion of the relative merits of one-sided and two-sided tests is given in Armitage and Berry (1987) and Kirkwood and Sterne (2003).

