21.5: Analysis of rates
- Page ID
- 13732
5.1 Risks, rates, and person-time-at-risk
The terms ‘risk’ and ‘rate’ are often used rather loosely and interchangeably to describe the frequencies of events in epidemiological studies. Usually, this is of no great consequence, but, in some circumstances, the distinction is important and, in particular, may affect the way in which a study is analysed. A risk is essentially a proportion, or equivalently a probability. The numerator consists of the number of individuals who experience the event of interest (say, develop the disease) in a defined period. The denominator consists of the total number of individuals who were followed for the defined period, some of whom experienced the event of interest (for example, developed the disease) and the remainder of whom did not (ignoring, for the moment, complications that might arise if some individuals are lost to follow-up). A rate takes into account both the number of persons at risk and also the duration of observation for each person. In the simplest case, the numerator is the number of individuals who experience the event of interest during the study period (i.e. the same as the numerator for a risk), but the denominator is expressed as the person-time (for example, person-years or person-days) at risk for the individuals in the study.
For example, if 120 persons are observed for 3 years and 40 of them die at some time during the period, and none are otherwise lost to follow-up, the risk of death over the 3 years is estimated as 40/120 = 0.33, whereas the death rate is estimated as 40/(the number of person-years-at-risk). The denominator for the rate calculation is (80 × 3) +(40 × 1.5) = 300 years, as 80 persons were ‘at risk’ for the full 3-year period, and 40 were at risk until they died (which, on average, is likely to have been about halfway through the follow-up period if deaths occurred uniformly over the period). Thus, the death rate is 40/300 = 0.133 per person-year-at-risk (which is not the same as the risk of death during the 3 years of 0.33 divided by 3).
Mathematically, it is straightforward to convert rates to risks, and vice versa, if it may be assumed that the rates are constant over time (see, for example, Breslow and Day, 1980). The reason for discussing the distinction in this chapter is that different methods of statistical analysis are appropriate for risks and rates. As mentioned in Section 4, risks are proportions, and thus the methods described in that section are applicable. Modifications of these methods are necessary for the analysis of rates.
Rates are useful if different individuals in a study have been followed for different periods. This may arise if recruitment to the study population is staggered over time, but follow-up is to a common date, or if individuals are lost to follow-up at different times (for example, because of death, migration, or non-co-operation).
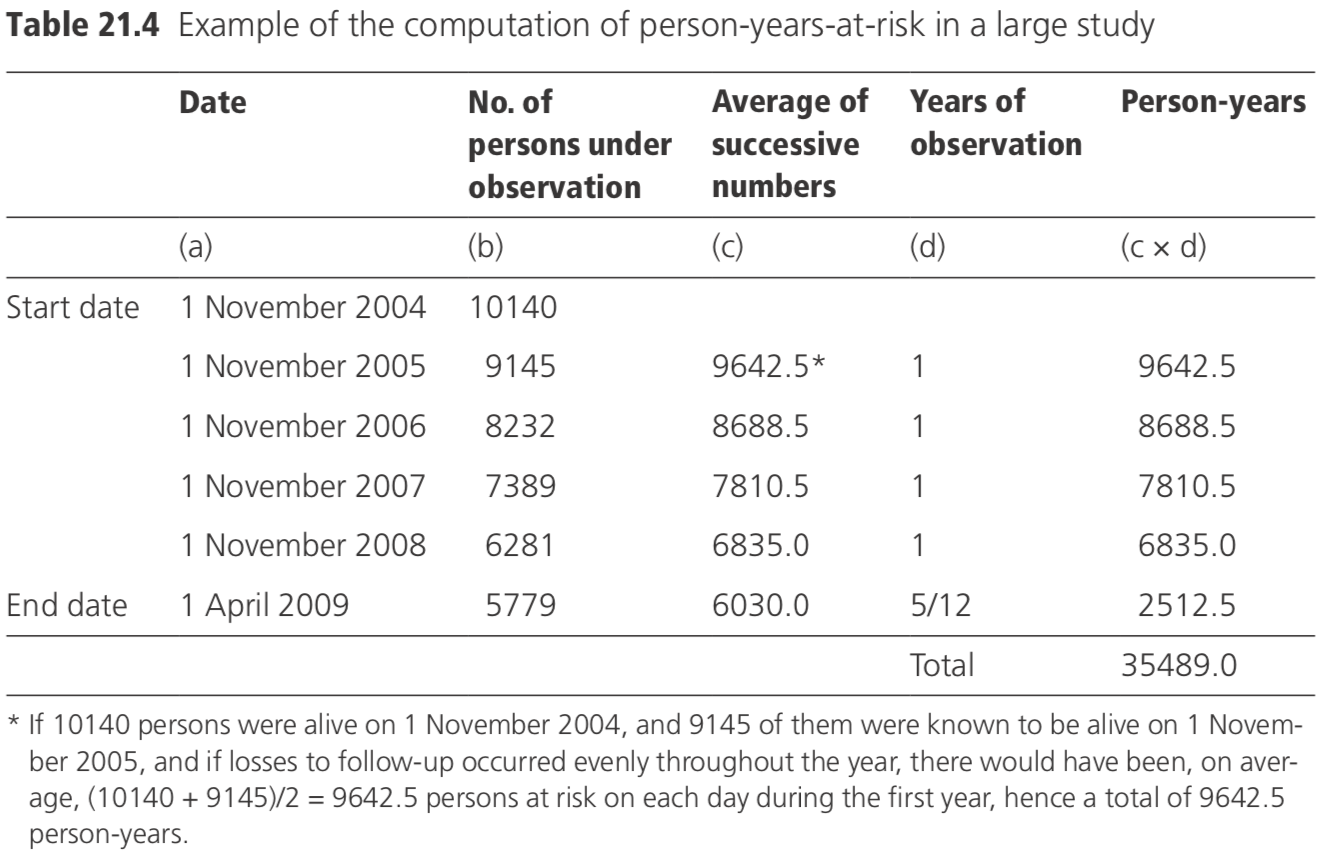
An example of the computation of person-years-at-risk in a large study is given in Table 21.4. In this study, a census was done of the study population on the 1 November each year, and the number of persons remaining at risk was ascertained.
Alternatively, the exact period of follow-up may be known for each subject in the study (if the dates of entry and exit are available for each person), in which case these periods would be summed to derive the total person-years-at-risk.
Another situation in which rates, rather than risks, may be more appropriate is when each individual may be at risk of experiencing the event of interest more than once during the study period (for example, an episode of diarrhoea). The incidence rate in the study population would be calculated as the total number of events (for example, episodes of diarrhoea) for those in the study divided by the total person-time-at-risk (which, in this case, would not end at the first episode). Responses such as this can always be converted to a risk by expressing the outcome as the proportion of individuals who experience more than a specified number of events (for example, one or more episodes of diarrhoea), but, in doing this, some information is lost, with a consequent reduction in the power of the study to detect a difference between groups being compared. The analysis of rate data of this kind (where one individual may experience more than one episode of disease) is not straightforward, as the approach depends upon whether it is reasonable to assume that, once an individual has experienced one event, he or she is no more or less likely to experience another event than anyone else in the same intervention group (say, of the same age and sex). Usually, it is not reasonable to make this assumption, as it is frequently found that susceptibility and exposure to disease vary considerably between individuals in ways that cannot be predicted. A simple way out of the analytical problem is to classify individuals, according to whether or not they experienced any events or not. If this is done, the data can either be analysed as a proportion (using the methods given in Section 4) or the individual can be excluded from follow-up for purposes of analysis, from the time the first event occurs (i.e. they are not counted as ‘at risk’ after the first event), and the methods given in Sections 5.2 to 5.5 can be used.
5.2 Confidence interval for a rate
Suppose e is the number of events that occurred during the study period, and the total person-years-at-risk during the period was y. (Note that the period does not have to be measured in ‘years’; it could be in, for example, days, weeks, or months.) The event rate (r) is estimated by e/y. For example, suppose 5000 patients who have received a new tuberculosis (TB) vaccine have been followed for 5 years, but, due to losses in follow- up, the total person-years-at-risk is 20 000 (instead of the nearly 25 000 that would have been appropriate if every patient—except the cases whose follow-up period would be counted up to the time they developed TB—had been followed up throughout the 5 years). If the number of new cases of TB that were detected during the follow-up was 80, the estimated incidence rate of TB would be 80/20 000 = 0.0040/person-year, i.e. four per thousand person-years.
The standard error of a rate (r) is, √(r/y) and the approximate 95% CI for the rate is given by r ± 1.96√(r/y). Thus, in the TB example, the 95% CI for the TB incidence rate is:
\[
0.0040+1.96 \sqrt{(0.0040 / 20 ~ 000)}=0.0040 \pm 0.0009
\]
i.e. 3.1–4.9 per thousand person-years.
5.3 Difference between two rates
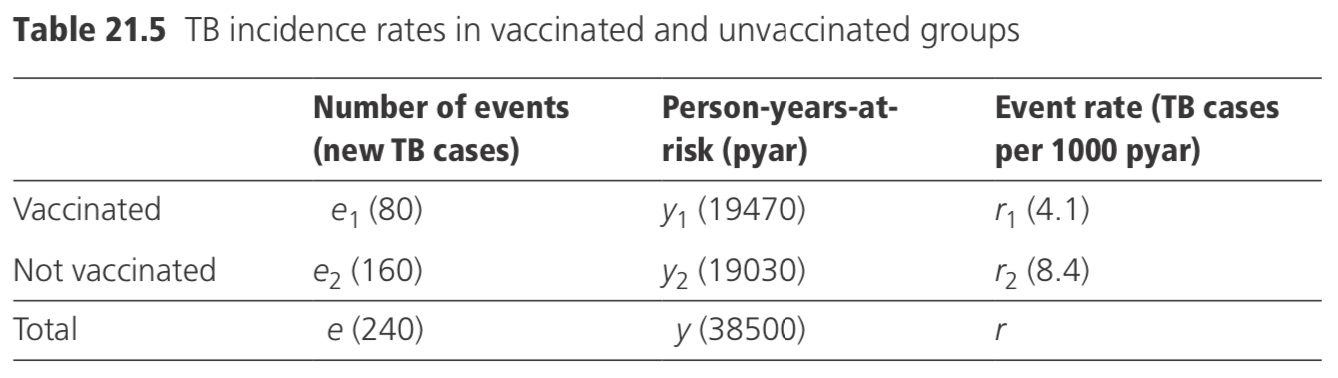
Suppose it is required to compare event rates in two groups, and the number of events and the person-years-at-risk in the two groups are as in Table 21.5.
The standard error of the difference between two rates is given by: \(\sqrt{( } r_{1} / y_{1}+r_{2} y_{2} )\), and the 95% CI on the difference is given by \(\left(r_{1}-r_{2}\right) \pm 1.96\) SE.
Thus, for the example, the 95% CI on the rate difference of the vaccinated, compared to the unvaccinated, group in Table 21.5 is:
\[\begin{align}(0.0041−0.0084)±1.96√[(0.0041/19 470)+(0.0084/19 030)] & =−0.0043±0.0016 \\ &=−0.0059 to −0.0027 \end{align}\]
i.e. −5.9 to −2.7/1000/year.
To perform a statistical test, it is necessary to calculate a test statistic, which may be done along similar lines to those described in Section 4.2. If e1 is the observed number of events among those in group 1 (say, those vaccinated), then:
\[
\text { Expected value of } e_{1}=E\left(e_{1}\right)=e y_{1} / y
\]
\[
\text { Variance of } e_{1}=V\left(e_{1}\right)=e y_{1} y_{2} / y^{2}
\]
Then:
\[
\chi^{2}=\left(\left|e_{1}-E\left(e_{1}\right)\right|-0.5\right)^{2} / V\left(e_{1}\right)
\]
And the value of χ2 is looked up in tables of the χ2 distribution, with one df, to assess the p-value.
In the example shown in Table 21.5, \(e_{1}=80 E\left(e_{1}\right)=240 \times 19470 / 38500=121.37\)and \(V\left(e_{1}\right)=(240 \times 19 \quad 470) /(38500 \times 38 \quad 500)=59.99\)
Thus, \(\chi^{2}=(|80-121.37|-0.5)^{2} / 59.99=27.84\), and p < 0.000001, indicating that the difference is highly unlikely to have arisen by chance.
5.4 Ratio of two rates
In some situations, the ratio of two rates will be of greater interest than their difference. For example, vaccine efficacy is usually calculated from a ratio. The test of the null hypothesis is identical in the two situations (i.e. the difference is zero, or the ratio is unity), but the CIs are calculated in a different way.
The ratio of two rates, sometimes called the relative risk, but more correctly called the relative rate, is \(\left(e_{1} / y_{1}\right) /\left(e_{2} / y_{2}\right)\), and the standard error of the logarithm of this ratio is approximated by \(√[(1/e_1)+(1/e_2)]\). In the example given in Table 21.5, the ratio of the rates is 0.489 (corresponding to a vaccine efficacy of 51.1%), and the standard error of the logarithm of the ratio is \(√[(1/80)+(1/160)]= 0.1369\). The 95% CI of the logarithm of the ratio is given by \(−0.715±1.96(0.1369)\), i.e. −0.983 to −0.447. Thus, the 95% CI for the ratio of the two rates is 0.37–0.64 (or the 95% CI on the estimate of vaccine efficacy is from 36% to 63%, i.e. 100(1−0.64) to 100(1−0.37).
5.5 Trend test for rates
Directly analogous to the trend test for proportions described in Section 4.4, there is a similar test for a trend in rates. Suppose data have been collected from the time since the start of a study to the first attack of malaria among children of different ages, and it is of interest to test whether the attack rate declines with age. The data may be summarized, as in Table 21.6.
A ‘score’ has been assigned to each group. In the example, the scores have been taken as the mid points of the different age groups (for example, those aged 1–2 years range in age from 1.00 to 2.99 years).
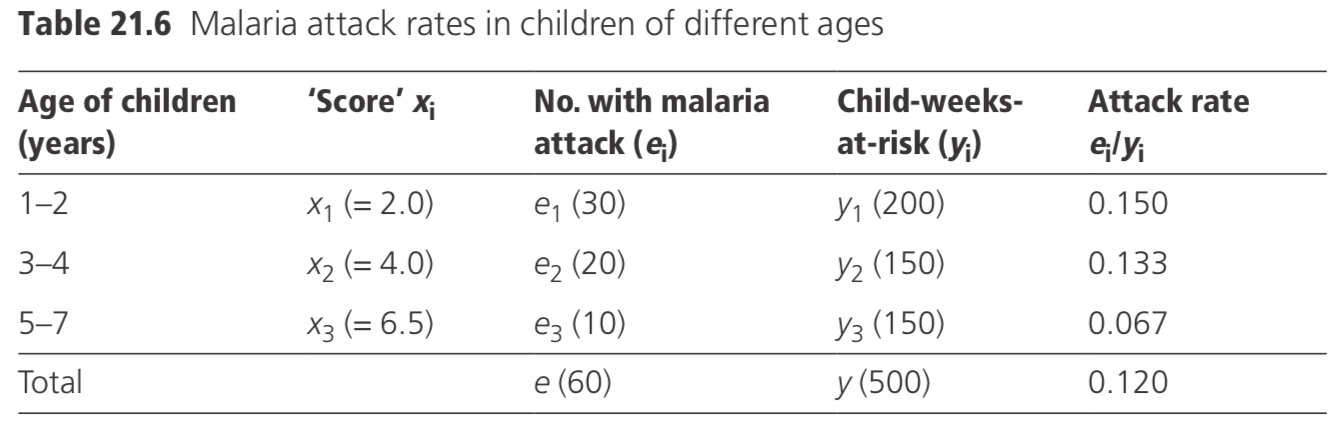
Table 21.7 ESR in an intervention and a control group
| Intervention group (i = 1) | Control group (i = 2) | |
|---|---|---|
| Number of subjects (\(n^i\)) | 10 | 12 |
| Mean ESR (\(\overline{x}^i\)) | 9.7 | 6.5 |
| Standard deviation (\(s^i\)) | 2.41 | 2.54 |
A test for trend in the attack rates in the three age groups \(e_{1} / y_{1}, e_{2} / y_{2}\) and \(e_{3} / y_{3}\) is provided by testing the expression, as χ2 with one df:
\[
\chi^{2}=\left\{\left[\Sigma e_{\mathrm{i}} x_{\mathrm{i}}-\left[(e / y) \Sigma y_{\mathrm{i}} x_{\mathrm{i}}\right]\right\}^{2} /\left\{\left(e / y^{2}\right)\left[y \Sigma y_{\mathrm{i}} x_{\mathrm{i}}^{2}-\left(\Sigma y_{\mathrm{i}} x_{\mathrm{i}}\right)^{2}\right]\right\}\right.
\]
For example, suppose the malaria attack rates (attacks/weeks-at-risk) were as in Table 21.6, then the value of χ2 is:
\[
\{205-[(60 / 500) 1975]\}^{2} /\left\{\left(60 \times 500^{2}\right) \quad\left[(500 \times 9537.5)-1975^{2}\right]\right\}=4.91
\]
which has an associated p-value of 0.03, and thus there are grounds for believing that, in the study area, the risk of a malaria attack declined with increasing age.

