5.2: Criteria for determining trial size
- Page ID
- 13159
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)2.1 Precision of effect measures
To select the appropriate sample size, it is necessary to decide how much sampling error in the estimate of the effect of the intervention is acceptable and to select the sample size to achieve this precision. When the data are analysed, the amount of sampling error is represented by the width of the confidence interval around the estimate of effect. The narrower the CI, the greater the precision of the estimate, and the smaller the probable amount of sampling error. When designing a trial, it is necessary therefore to decide the width of an acceptable CI around the chosen intervention effect. Having made this decision, the method to select the required trial size is given in Section 3.
2.2 Power of the trial
An alternative approach is to choose a trial size which gives adequate power to detect an effect of a given magnitude. The focus is then on the result of the significance test which will be conducted at the end of the trial. The significance test assesses the evidence against the null hypothesis, which states that there is no true difference between the interventions under comparison. A statistically significant result indicates that the data conflict with the null hypothesis and that there are grounds for rejecting the hypothesis that there is no difference in the effects of the interventions under study on the outcomes of interest.
Because of the variations resulting from sampling error, it is never possible to be certain of obtaining a significant result at the end of a trial, even if there is a real difference. It is necessary to consider the probability of obtaining a statistically significant result in a trial, and this probability is called the power of the trial. Thus, a power of 80% to detect a difference of a specified size means that, if the trial were to be conducted repeatedly, a statistically significant result would be obtained four times out of five (80%) if the true difference was really of the specified size. The power of a trial depends on the factors shown in Box 5.1.
The power also depends on whether a one-sided or two-sided significance test is to be performed (see Chapter 21, Section 2.3) and on the underlying variability of the data. How the power may be calculated for given values of these parameters is explained in Section 4.
When designing a trial, the objective is to ensure that the trial size is large enough to give high power if the true effect of the intervention is large enough to be of public health importance.
2.3 Choice of criterion
The choice of which criterion (precision or power) should be used in any particular trial depends on the objectives of the trial. If it is known unambiguously that the intervention has some effect (relative to the comparison (control) group), it makes little sense to test the null hypothesis; rather the objective may be to estimate the magnitude of the effect and to do this with some acceptable specified precision.
In trials of new interventions, it is often not known whether there will be any impact at all of the intervention on the outcomes of interest, and what is required is ‘proof of concept’. In these circumstances, it may be sufficient to ensure that there will be a good chance of obtaining a significant result if there is indeed an effect of some specified magnitude. It should be emphasized, however, that, if this course is adopted, the estimates obtained may be very imprecise. To illustrate this, suppose it is planned to compare two groups with respect to the mean of some variable, and suppose the true difference between the group means is D. If the trial size is chosen to give 90% power (of obtaining a significant difference with p<0.05p<0.05on a two-sided test) if the difference is D, the 95% CI on D is expected to extend roughly from 0.4 D to 1.6 D. This is a wide range and implies that the estimate of the effect of intervention will be imprecise. In many situations, it may be more appropriate to choose the sample size by setting the width of the CI, rather than to rely on power calculations.
Box 5.1 The power of the trial depends on:
- The value of the true difference between the study groups, in other words, the true effect of the intervention. The greater the effect, the higher the power to detect the effect as statistically significant for a trial of a given size.
- The trial size. The larger the trial size, the higher the power.
- The probability level (p-value) at which a difference will be regarded as ‘statistically significant’.
2.4 Trials with multiple outcomes
The discussion in Sections 2.1 to 2.3 concerns factors influencing the choice of trial size, with respect to a particular outcome measure. In most trials, several different outcomes are measured. For example, in a trial of the impact of insecticide-treated mosquito-nets on childhood malaria, there may be interest in the effects of the intervention on deaths, deaths attributable to malaria, episodes of clinical malaria, spleen sizes at the end of the malaria season, PCVs at the end of the malaria season, and possibly other measures.
Chapter 12, Section 2 highlights the importance of defining in advance the primary outcome and a limited number of secondary outcomes of a trial. In order to decide on the trial size, the investigator should first focus attention on the primary outcome, as results for this outcome will be given the most weight when reporting the trial findings, and it is essential that the trial is able to provide adequate results for this outcome. The methods of this chapter can then be used to calculate the required trial size for the primary outcome and each of the secondary outcomes.
Ideally, the outcome that results in the largest trial size would be used to determine the size, as then, for other outcomes, it would be known that better than the required precision or power would be achieved. It is often found, however, that one or more of the outcomes would require a trial too large for the resources that are likely to be available. For example, detecting changes in mortality, or cause-specific mortality, often requires very large trials. In these circumstances, it may be decided to design the trial to be able to detect an impact on morbidity and accept that it is unlikely to be able to generate conclusive findings about the effect on mortality. It is important to point out, however, that, if a trial shows that an intervention has an impact on morbidity, it may be regarded as unethical to undertake a further, larger trial to assess the impact on mortality. For this reason, it is generally advisable to ensure that trials are conducted at an early stage in which the outcome of greatest public health importance is the endpoint around which the trial is planned. This issue is discussed further in Chapter 6.
Sometimes, different trial sizes may be used for different outcomes. For example, it might be possible to design a trial in such a way that a large sample of participants are monitored for mortality, say by annual surveys, and only a proportion of participants are monitored for morbidity, say by weekly visits.
If it is not feasible to design the trial to achieve adequate power or precision for the primary outcome, the trial should either be abandoned or a different primary outcome should be adopted.
2.5 Practical constraints
In practice, statistical considerations are not the only factors that need to be taken into account in planning the size of an investigation. Resources, in terms of staff, vehicles, laboratory capacity, time, or money, may limit the potential size of a trial, and it is often necessary to compromise between the results of the trial size computations and what can be managed with the available resources. Trying to do a trial that is beyond the capacity of the available resources is likely to be unfruitful, as data quality is likely to suffer and the results may be subject to serious bias, or the trial may even collapse completely, wasting the effort and money that have already been expended. If calculations indicate that a trial of manageable size will yield power and/or precision that is unacceptably low, it is probably better not to conduct the trial at all.
A useful approach to examine the trade-off between trial size (and thus cost) and power is to construct power curves for one or two of the key outcome variables. Power curves show how power varies with trial size for different values of the effect measure. Figure 5.1 shows power curves for malaria deaths in the mosquito-net trial discussed in Section 2.4, assuming that equal numbers of children are to be allocated to the intervention and control groups and statistical significance is to be based on a two-sided test at the 5% level. R represents the rate ratio of malaria deaths in the intervention group, compared to the control group, so that R=0.3R=0.3represents a reduction in the death rate of 70%. The assumptions used to construct these curves are described in Section 4. The curves indicate that, if 1000 children were followed for 1 year in each group (making 2000 children in all), there would be about a one in two chance of obtaining a significant result (power = 50%), even if the reduction in the death rate was as high as 70%. A trial five times as large as this would have a good chance (about 80%) of detecting a reduction in the death rate of 50% or more but would be inadequate (about 40%) to detect a 30% reduction in the death rate.
Figure 5.1 Power curves for a trial of the effect of mosquito-nets on malaria deaths.
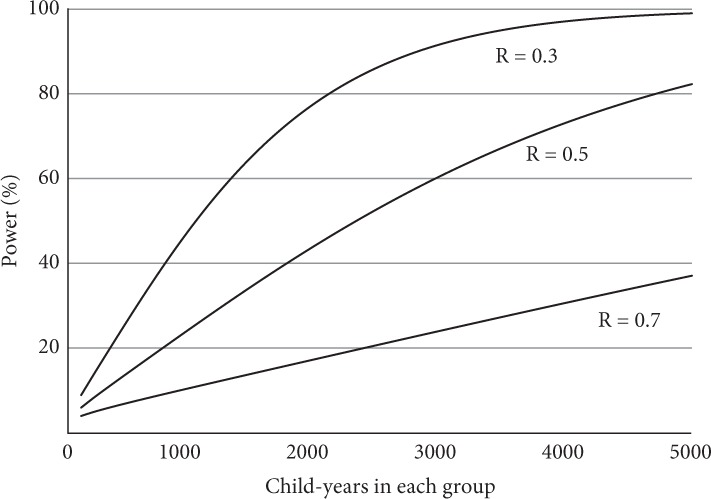
Malaria death rate in the control group assumed to be 10/1000/year. R, relative rate in the intervention group. Assumes equal-sized groups, two-sided test, and significance p < 0.05.

