4.2: Biology of Synaptic Plasticity
- Page ID
- 12581
Learning amounts to changing the overall synaptic efficacy of the synapse connecting two neurons. The synapse has a lot of moving parts (see Neuron/Biology), any one of which could potentially be the critical factor in causing its overall efficacy to change. How many can you think of? The search for the critical factor(s) dominated the early phase of research on synaptic plasticity, and evidence for the involvement of a range of different factors has been found over the years, from the amount of presynaptic neurotransmitter released, to number and efficacy of postsynaptic AMPA receptors, and even more subtle things such as the alignment of pre and postsynaptic components, and more dramatic changes such as the cloning of multiple synapses. However, the dominant factor for long-lasting learning changes appears to be the number and efficacy of postsynaptic AMPA receptors.

Figure 4.1 shows the five critical steps in the cascade of events that drives change in AMPA receptor efficacy. The NMDA receptors and the calcium ion (Ca++) play a central role -- NMDA channels allow Ca++ to enter the postsynaptic spine. Across all cells in the body, Ca++ typically plays an important role in regulating cellular function, and in the neuron, it is capable of setting off a series of chemical reactions that ends up controlling how many AMPA receptors are functional in the synapse. For details on these reactions, see Detailed Biology of Learning. Here's what it takes for the Ca++ to get into the postsynaptic cell:
- The postsynaptic membrane potential (Vm) must be elevated, as a result of all the excitatory synaptic inputs coming into the cell. The most important contributor to this Vm level is actually the backpropagating action potential -- when a neuron fires an action potential, it not only goes forward out the axon, but also backward down the dendrites (via active voltage-sensitive Na+ channels along the dendrites). Thus, the entire neuron gets to know when it fires -- we'll see that this is incredibly useful computationally.
- The elevated Vm causes magnesium ions (Mg+) to be repelled (positive charges repel each other) out of the openings of NMDA channels, unblocking them.
- The presynaptic neuron fires an action potential, releasing glutamate neurotransmitter into the synaptic cleft.
- Glutamate binds to the NMDA receptor, opening it to allow Ca++ ions to flow into the postsynaptic cell. This only occurs if the NMDA is also unblocked. This dependence of NMDA on both pre and postsynaptic activity was one of the early important clues to the nature of learning, as we see later.
- The concentration of Ca++ in the postsynaptic spine drives those complex chemical reactions (Detailed Biology of Learning) that end up changing the number and efficacy of AMPA receptors. Because these AMPA receptors provide the primary excitatory input drive on the neuron, changing them changes the net excitatory effect of a presynaptic action potential on the postsynaptic neuron. This is what is meant by changing the synaptic efficacy, or weight.
Ca++ can also enter the postsynaptic cell via voltage gated calcium channels (VGCC)'s which are calcium channels that only open when the membrane potential is elevated. Unlike NMDA, however, they are not sensitive to presynaptic neural activity -- they only depend on postsynaptic activity. This has important computational implications, as we discuss later. VGCC's contribute less to Ca++ levels than NMDA, so NMDA is still the dominant player.
Metabotropic glutamate receptors (mGlu) also play an important role in synaptic plasticity. These receptors do not allow ions to flow across the membrane (i.e., they are not ionotropic), and instead they directly trigger chemical reactions when neurotransmitter binds to them. These chemical reactions can then modulate the changes in AMPA receptors triggered by Ca++.
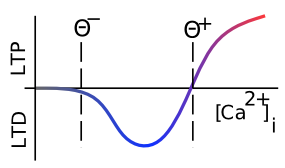
We have been talking about changes in AMPA receptor efficacy without specifying which direction they change. Long Term Potentiation (LTP) is the biological term for long-lasting increases in AMPA efficacy, and Long Term Depression (LTD) means long-lasting decreases in AMPA efficacy. For a long time, researchers focused mainly on LTP (which is generally easier to induce), but eventually they realized that both directions of synaptic plasticity are equally important for learning. Figure 4.2 shows how this direction of change depends on the overall level of Ca++ in the postsynaptic spine (accumulated over a few 100's of milliseconds at least -- the relevant time constants for effects of Ca++ on synaptic plasticity are fairly slow) -- low levels drive LTD, while high levels produce LTP. This property will be critical for our computational model. Note that the delay in synaptic plasticity effects based on Ca++ levels means that the synapse doesn't always have to do LTD on its way up to LTP -- there is time for the Ca++ to reach a high level to drive LTP before the weights start to change.
Hebbian Learning and NMDA Channels
The famous Canadian psychologist Donald O. Hebb predicted the nature of the NMDA channel many years in advance of its discovery, just by thinking about how learning should work at a functional level. Here is a key quote:
- Let us assume that the persistence or repetition of a reverberatory activity (or "trace") tends to induce lasting cellular changes that add to its stability.… When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A's efficiency, as one of the cells firing B, is increased.
This can be more concisely summarized as cells that fire together, wire together. The NMDA channel is essential for this process, because it requires both pre and postsynaptic activity to allow Ca++ to enter and drive learning. It can detect the coincidence of neural firing. Interestingly, Hebb is reputed to have said something to the effect of "big deal, I knew it had to be that way already" when someone told him that his learning principle had been discovered in the form of the NMDA receptor.
Mathematically, we can summarize Hebbian learning as:
- \(\Delta w=x y\)
where \(\Delta w\) is the change in synaptic weight w, as a function of sending activity \(x\) and receiving activity \(y\).
Anytime you see this kind of pre-post product in a learning rule, it tends to be described as a form of Hebbian learning. For a more detailed treatment of Hebbian learning and various popular variants of it, see Hebbian Learning .
As we'll elaborate below, this most basic form of Hebbian learning is very limited, because weights will only go up (given that neural activities are rates of spiking and thus only positive quantities), and will do so without bound. Interestingly, Hebb himself only seemed to have contemplated LTP, not LTD, so perhaps this is fitting. But it won't do anything useful in a computational model. Before we get to the computational side of things, we cover one more important result in the biology.
Spike Timing Dependent Plasticity
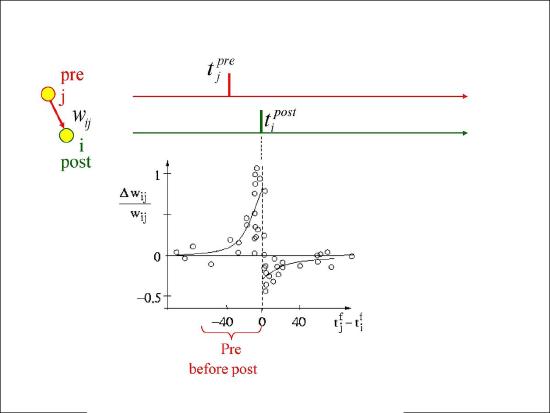
Figure 4.3 shows the results from an experiment by Bi and Poo in 1998 that captured the imagination of many a scientist, and has resulted in extensive computational modeling work. This experiment showed that the precise order of firing between a pre and postsynaptic neuron determined the sign of synaptic plasticity, with LTP resulting when the presynaptic neuron fired before the postsynaptic one, while LTD resulted otherwise. This spike timing dependent plasticity (STDP) was so exciting because it fits with the causal role of the presynaptic neuron in driving the postsynaptic one. If a given pre neuron actually played a role in driving the post neuron to fire, then it will necessarily have to have fired in advance of it, and according to the STDP results, its weights will increase in strength. Meanwhile, pre neurons that have no causal role in firing the postsynaptic cell will have their weights decreased. However, as we discuss in more detail in STDP, this STDP pattern does not generalize well to realistic spike trains, where neurons are constantly firing and interacting with each other over 100's of milliseconds. Nevertheless, the STDP data does provide a useful stringent test for computational models of synaptic plasticity. We base our learning equations on a detailed model using more basic, biologically-grounded synaptic plasticity mechanisms that does capture these STDP findings (Urakubo, Honda, Froemke, & Kuroda, 2008), but which nevertheless result in quite simple learning equations when considered at the level of firing rate.