7.1: Electrical Potential
- Page ID
- 9576
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describe membrane potential in terms of variables in Ohm’s Law
Ohm’s Law
What drives current? We can think of various devices—such as batteries, generators, wall outlets, and so on—which are necessary to maintain a current. All such devices create a potential difference and are loosely referred to as voltage sources. When a voltage source is connected to a conductor, it applies a potential difference \(V\) that creates an electric field. The electric field in turn exerts force on charges, causing current.
The current that flows through most substances is directly proportional to the voltage \(V\) applied to it. The German physicist Georg Simon Ohm (1787–1854) was the first to demonstrate experimentally that the current in a metal wire is directly proportional to the voltage applied:
\[T \propto V\]
This important relationship is known as Ohm’s law. It can be viewed as a cause-and-effect relationship, with voltage the cause and current the effect. This is an empirical law like that for friction—an experimentally observed phenomenon. Such a linear relationship doesn’t always occur.
Resistance and Simple Circuits
If voltage drives current, what impedes it? The electric property that impedes current (crudely similar to friction and air resistance) is called resistance \(R\) Collisions of moving charges with atoms and molecules in a substance transfer energy to the substance and limit current. Resistance is defined as inversely proportional to current, or
\[ I \propto \dfrac{1}{R}\]
Thus, for example, current is cut in half if resistance doubles. Combining the relationships of current to voltage and current to resistance gives
\[I = \dfrac{V}{R}\]
This relationship is also called Ohm’s law. Ohm’s law in this form really defines resistance for certain materials. Ohm’s law (like Hooke’s law) is not universally valid. The many substances for which Ohm’s law holds are called ohmic. These include good conductors like copper and aluminum, and some poor conductors under certain circumstances. Ohmic materials have a resistance that is independent of voltage
and current
. An object that has simple resistance is called a resistor, even if its resistance is small. The unit for resistance is an ohm and is given the symbol
(upper case Greek omega). Rearranging
gives
, and so the units of resistance are 1 ohm = 1 volt per ampere:
\[1 = 1 \dfrac{V}{A}\]
Figure 7.1 shows the schematic for a simple circuit. A simple circuit has a single voltage source and a single resistor. The wires connecting the voltage source to the resistor can be assumed to have negligible resistance, or their resistance can be included in .
A simple electric circuit in which a closed path for current to flow is supplied by conductors (usually metal wires) connecting a load to the terminals of a battery, represented by the red parallel lines. The zigzag symbol represents the single resistor and includes any resistance in the connections to the voltage source.
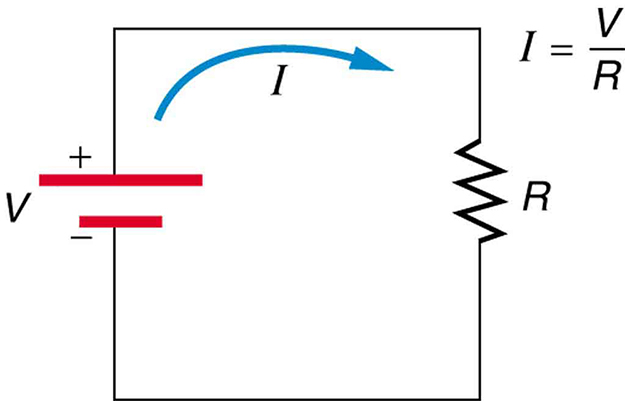
Resistances range over many orders of magnitude. Some ceramic insulators, such as those used to support power lines, have resistances of or more. A dry person may have a hand-to-foot resistance of
, whereas the resistance of the human heart is about
. A meter-long piece of large-diameter copper wire may have a resistance of
, and superconductors have no resistance at all (they are non-ohmic). Resistance is related to the shape of an object and the material of which it is composed.
Additional insight is gained by solving for
yielding
\[V = IR\]
Figure 7.2. The voltage drop across a resistor in a simple circuit equals the voltage output of the battery.
In a simple electrical circuit, the sole resistor converts energy supplied by the source into another form. Conservation of energy is evidenced here by the fact that all of the energy supplied by the source is converted to another form by the resistor alone. We will find that conservation of energy has other important applications in circuits and is a powerful tool in circuit analysis.
Nerve Conduction
Electric currents in the vastly complex system of billions of nerves in our body allow us to sense the world, control parts of our body, and think. These are representative of the three major functions of nerves. First, nerves carry messages from our sensory organs and others to the central nervous system, consisting of the brain and spinal cord. Second, nerves carry messages from the central nervous system to muscles and other organs. Third, nerves transmit and process signals within the central nervous system. The sheer number of nerve cells and the incredibly greater number of connections between them makes this system the subtle wonder that it is. Nerve conduction is a general term for electrical signals carried by nerve cells. It is one aspect of bioelectricity, or electrical effects in and created by biological systems.
Nerve cells, properly called neurons, look different from other cells—they have tendrils, some of them many centimeters long, connecting them with other cells (Figure 7.3). Signals arrive at the cell body across synapses or through dendrites, stimulating the neuron to generate its own signal, sent along its long axon to other nerve or muscle cells. Signals may arrive from many other locations and be transmitted to yet others, conditioning the synapses by use, giving the system its complexity and its ability to learn.
A neuron with its dendrites and long axon. Signals in the form of electric currents reach the cell body through dendrites and across synapses, stimulating the neuron to generate its own signal sent down the axon. The number of interconnections can be far greater than shown here.

The method by which these electric currents are generated and transmitted is more complex than the simple movement of free charges in a conductor, but it can be understood with principles already discussed in this text. The most important of these are the Coulomb force and diffusion.
Figure 7.4 illustrates how a voltage (potential difference) is created across the cell membrane of a neuron in its resting state. This thin membrane separates electrically neutral fluids having differing concentrations of ions, the most important varieties being ,
, and
(these are sodium, potassium, and chlorine ions with single plus or minus charges as indicated). Free ions will diffuse from a region of high concentration to one of low concentration. But the cell membrane is semipermeable, meaning that some ions may cross it while others cannot. In its resting state, the cell membrane is permeable to
and
, and impermeable to
. Diffusion of
and
thus creates the layers of positive and negative charge on the outside and inside of the membrane. The Coulomb force prevents the ions from diffusing across in their entirety. Once the charge layer has built up, the repulsion of like charges prevents more from moving across, and the attraction of unlike charges prevents more from leaving either side. The result is two layers of charge right on the membrane, with diffusion being balanced by the Coulomb force. A tiny fraction of the charges move across and the fluids remain neutral (other ions are present), while a separation of charge and a voltage have been created across the membrane.
Figure 7.4. The process of how a voltage (potential difference) is created across the cell membrane of a neuron in its resting state.
Describe electrical signal in a cell using the following terms: resistance, flow, and potential difference
Which cells are involved in maintaining electrical potential of an animal cell and how


