2.6: Atomic Masses
- Page ID
- 15209
- Define atomic mass and atomic mass unit.
- Calculate atomic mass.
Even though atoms are very tiny pieces of matter, they have mass. Their masses are so small, however, that chemists often use a unit other than grams to express them—the atomic mass unit.
Atomic Mass Unit
The atomic mass unit (abbreviated u, although amu is also used) is defined as 1/12 of the mass of a 12C atom:
\[\mathrm{1\:u=\dfrac{1}{12}\textrm{ the mass of }^{12}C\:atom} \label{Eq1} \]
It is equal to 1.661 × 10−24 g.
Masses of other atoms are expressed with respect to the atomic mass unit. For example, the mass of an atom of 1H is 1.008 u, the mass of an atom of 16O is 15.995 u, and the mass of an atom of 32S is 31.97 u. Note, however, that these masses are for particular isotopes of each element. Because most elements exist in nature as a mixture of isotopes, any sample of an element will actually be a mixture of atoms having slightly different masses (because neutrons have a significant effect on an atom’s mass). How, then, do we describe the mass of a given element? By calculating an average of an element’s atomic masses, weighted by the natural abundance of each isotope, we obtain a weighted average mass called the atomic mass (also commonly referred to as the atomic weight) of an element.
Atomic Mass is the Weighted Average Mass of Isotopes
As stated above, most elements occur naturally as a mixture of two or more isotopes. Listed below (Table \(\PageIndex{1}\)) are the naturally occurring isotopes of selected elements along with the percent natural abundance of each.
| Element | Isotope (Symbol) | Percent Natural Abundance | Atomic Mass \(\left( \text{amu} \right)\) | Average Atomic Mass \(\left( \text{amu} \right)\) |
|---|---|---|---|---|
| Hydrogen | \(\ce{_1^1H}\) | 99.985 | 1.0078 | 1.0079 |
| \(\ce{_1^2H}\) | 0.015 | 2.0141 | ||
| \(\ce{_1^3H}\) | negligible | 3.0160 | ||
| Carbon | \(\ce{_6^{12}C}\) | 98.89 | 12.000 | 12.011 |
| \(\ce{_6^{13}C}\) | 1.11 | 13.003 | ||
| \(\ce{_6^{14}C}\) | trace | 14.003 | ||
| Oxygen | \(\ce{_8^{16}O}\) | 99.759 | 15.995 | 15.999 |
| \(\ce{_8^{17}O}\) | 0.037 | 16.995 | ||
| \(\ce{_8^{18}O}\) | 0.204 | 17.999 | ||
| Chlorine | \(\ce{_{17}^{35}Cl}\) | 75.77 | 34.969 | 35.453 |
| \(\ce{_{17}^{38}Cl}\) | 24.23 | 36.966 | ||
| Copper | \(\ce{_{29}^{63}Cu}\) | 69.17 | 62.930 | 63.546 |
| \(\ce{_{29}^{65}Cu}\) | 30.83 | 64.928 |
For some elements, one particular isotope is much more abundant than any other isotopes. For example, naturally occurring hydrogen is nearly all hydrogen-1, and naturally occurring oxygen is nearly all oxygen-16. For many other elements, however, more than one isotope may exist in substantial quantities. Chlorine (atomic number 17) is yellowish-green toxic gas. About three quarters of all chlorine atoms have 18 neutrons, giving those atoms a mass number of 35. About one quarter of all chlorine atoms have 20 neutrons, giving those atoms a mass number of 37. Were you to simply calculate the arithmetic average of the precise atomic masses, you would get approximately 36.
\[\frac{34.969 \,u + 36.966 \,u}{2} = 35.968 \,u \nonumber \]
As you can see, the average atomic mass given in the last column of the table above (35.453) is significantly lower. Why? The reason is that we need to take into account the natural abundance percentages of each isotope in order to calculate what is called the weighted average. The atomic mass of an element is the weighted average of the atomic masses of the naturally occurring isotopes of that element.
\[0.7577 \left( 34.969 \,u \right) + 0.2423 \left( 36.966 \,u \right) = 35.453 \,u \nonumber \]
The weighted average is determined by multiplying the percent of natural abundance by the actual mass of the isotope. This is repeated until there is a term for each isotope. For chlorine, there are only two naturally occurring isotopes so there are only two terms.
Atomic mass = (%1)(mass 1) + (%2)(mass 2) + ⋯
Another example: oxygen exists as a mixture that is 99.759% 16O, 0.037% 17O and 0.204% 18O. The atomic mass of oxygen (use percent natural abundance data from Table 2.5.1) would be calculated as follows:
Atomic mass = (%1)(mass 1) + (%2)(mass 2) + (%3)(mass 3)
\[0.99759 \left( 15.995 u \right) + 0.00037 \left( 16.995 u \right) +0.00204 \left( 17.999 u \right)= 15.999 u \nonumber \]
To confirm your answer, compare the calculated value to the weighted mass displayed on the periodic table.
Calculate the atomic mass of oxygen. Oxygen exists as a mixture of 3 isotopes. Their respective masses and natural abundance are shown below.
- 16O: 15.995 u (99.759%)
- 17O: 16.995 u (0.037%)
- 18O: 17.999 u (0.204%)
Solution
Multiply the isotope abundance by the actual mass of the isotope, and then sum up the products.
\[0.99759 \left( 15.995\, u \right) + 0.00037 \left( 16.995 \,u \right) +0.00204 \left( 17.999\, u \right)= 15.999\, u \nonumber \]
Exercise \(\PageIndex{1}\)
Calculate the atomic mass of copper. Copper exists as a mixture of 2 isotopes. Their respective masses and natural abundance are shown below.
- 63Cu: 62.930 u (69.17%)
- 65Cu: 64.928 u (30.83%)
- Answer
-
63.546 u
The atomic mass of each element is found under the element symbol in the periodic table. Examples are shown below. The atomic mass of tin (Sn) is 118.71 u while the atomic mass of carbon (C) is 12.011 u. On the other hand, the atomic number (Z) of each element is found above the atomic symbol.
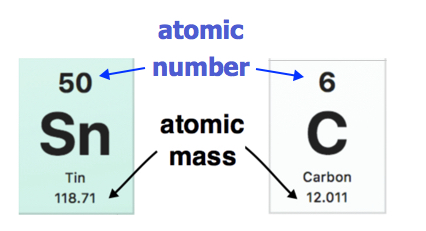
Atomic mass indicated on entries of the Periodic Table. (public Domain; Pubchem)
The periodic table is found in this link:
What is the average mass of a carbon atom in grams? The atomic mass is found in the Periodic Table. Please use two decimal places.
Solution
This is a simple one-step conversion, similar to conversions we did in Chapter 1. We use the fact that 1 u = 1.661 × 10−24 g:
\(\mathrm{12.01\:\cancel{u}\times\dfrac{1.661 \times 10^{-24}\:g}{1\:\cancel{u}}=1.995\times 10^{-23}\:g}\)
This is an extremely small mass, which illustrates just how small individual atoms are.
What is the average mass of a tin atom in grams? The average atomic mass is found in the Periodic Table. Please use two decimal places.
- Answer
-
\(\mathrm{118.71\:\cancel{u}\times\dfrac{1.661\times10^{-24}\:g}{1\:\cancel{u}}=1.972 \times 10^{-22}\:g}\)
Concept Review Exercises
- Define atomic mass. Why is it considered a weighted average?
- What is an atomic mass unit?
Answers
- The atomic mass is an average of an element’s atomic masses, weighted by the natural abundance of each isotope of that element. It is a weighted average because different isotopes have different masses.
- An atomic mass unit is 1/12th of the mass of a 12C atom.
Key Takeaway
- Atoms have a mass that is based largely on the number of protons and neutrons in their nucleus.
- The atomic mass of each element in the Periodic Table is the weighted average of the mass of all its isotopes.

