9.1C: Sliding Filament Model of Contraction
- Page ID
- 7529
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the sliding filament model, the thick and thin filaments pass each other, shortening the sarcomere.
- Describe the sliding filament model of muscle contraction
Key Points
- The sarcomere is the region in which sliding filament contraction occurs.
- During contraction, myosin myofilaments ratchet over actin myofilaments contracting the sarcomere.
- Within the sarcomere, key regions known as the I and H band compress and expand to facilitate this movement.
- The myofilaments themselves do not expand or contract.
Key Terms
- I-band: The area adjacent to the Z-line, where actin myofilaments are not superimposed by myosin myofilaments.
- A-band: The length of a myosin myofilament within a sarcomere.
- M-line: The line at the center of a sarcomere to which myosin myofilaments bind.
- Z-line: Neighbouring, parallel lines that define a sarcomere.
- H-band: The area adjacent to the M-line, where myosin myofilaments are not superimposed by actin myofilaments.
Movement often requires the contraction of a skeletal muscle, as can be observed when the bicep muscle in the arm contracts, drawing the forearm up towards the trunk. The sliding filament model describes the process used by muscles to contract. It is a cycle of repetitive events that causes actin and myosin myofilaments to slide over each other, contracting the sarcomere and generating tension in the muscle.
Sarcomere Structure
To understand the sliding filament model requires an understanding of sarcomere structure. A sarcomere is defined as the segment between two neighboring, parallel Z-lines. Z lines are composed of a mixture of actin myofilaments and molecules of the highly elastic protein titin crosslinked by alpha-actinin. Actin myofilaments attach directly to the Z-lines, whereas myosin myofilaments attach via titin molecules.
Surrounding the Z-line is the I-band, the region where actin myofilaments are not superimposed by myosin myofilaments. The I-band is spanned by the titin molecule connecting the Z-line with a myosin filament.
The region between two neighboring, parallel I-bands is known as the A-band and contains the entire length of single myosin myofilaments. Within the A-band is a region known as the H-band, which is the region not superimposed by actin myofilaments. Within the H-band is the M-line, which is composed of myosin myofilaments and titin molecules crosslinked by myomesin.
Titin molecules connect the Z-line with the M-line and provide a scaffold for myosin myofilaments. Their elasticity provides the underpinning of muscle contraction. Titin molecules are thought to play a key role as a molecular ruler maintaining parallel alignment within the sarcomere. Another protein, nebulin, is thought to perform a similar role for actin myofilaments.
Model of Contraction
The molecular mechanism whereby myosin and acting myofilaments slide over each other is termed the cross-bridge cycle. During muscle contraction, the heads of myosin myofilaments quickly bind and release in a ratcheting fashion, pulling themselves along the actin myofilament.
At the level of the sliding filament model, expansion and contraction only occurs within the I and H-bands. The myofilaments themselves do not contract or expand and so the A-band remains constant.
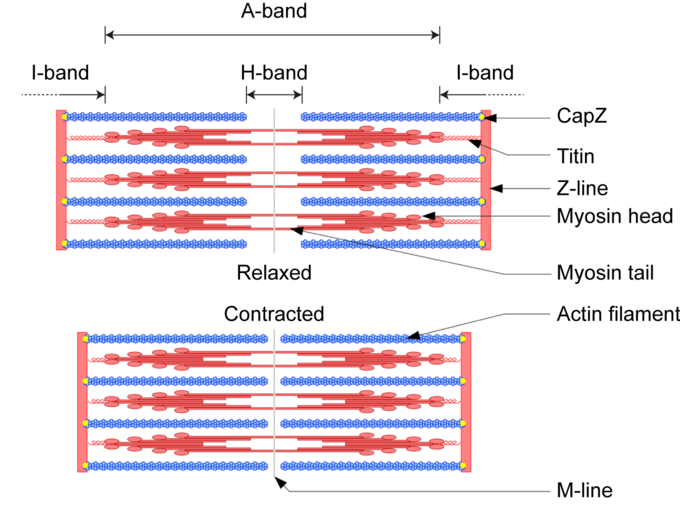
The sarcomere and the sliding filament model of contraction: During contraction myosin ratchets along actin myofilaments compressing the I and H bands. During stretching this tension is release and the I and H bands expand. The A-band remains constant throughout as the length of the myosin myofilaments does not change.
The amount of force and movement generated generated by an individual sarcomere is small. However, when multiplied by the number of sarcomeres in a myofibril, myofibrils in a myocyte and myocytes in a muscle, the amount of force and movement generated is significant.

