1.11: Screening and Diagnostic Testing
- Page ID
- 38524
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
After reading this chapter, you will be able to do the following:
- Differentiate between screening and diagnostic testing
- Calculate and interpret common test characteristics
- Discuss the role of public health in screening programs
Dx = disease
Sx = symptoms
Hx = history
Tx = treatment
Sn = sensitivity
Sp = specificity
PPV = positive predictive value
NPV = negative predictive value
Pt = patient.
Introduction
In this chapter, we will cover both screening and diagnostic testing. Though public health professionals are not usually directly involved with diagnosing patients, the tests used for screening and diagnostic testing are often the same (the difference being context), and the same mathematical tools are used to assess the accuracy of these tests. In addition, public health professionals who are involved in disease surveillance may need to know how to interpret these results when evaluating surveillance case definitions.
Screening versus Diagnostic Testing
The word screening refers to testing an asymptomatic population for a particular condition in order to identify those who have the condition so that they can be treated early. Common screening tests currently used in the US include various cancer screenings (mammograms, pap smears, skin checks for those at high risk of melanoma); routine hypertension screening at doctors’ offices (this is why they take your blood pressure every time you go); hearing, vision, and dental screening at elementary schools; annual tuberculosis and HIV screening among health care workers, and so on. Public health officials are often involved in screening programs either directly (providing personnel to go to the elementary school to conduct the hearing screenings) or indirectly (health education campaigns to increase the use of pap smears).
Diagnostic testing, on the other hand, is performed on a patient who is symptomatic in order to determine what condition they have. Clinicians perform what is called differential diagnosis when confronted with a patient with new complaints. In a nutshell, the doctor, nurse practitioner, or other health care provider takes all known information from the patient’s history and physical exam and decides what could be wrong. For instance, if a 24-year-old female presents to the clinic complaining of visual disturbances followed by severe headache, this could be any number of things: concussion, migraine with aura, hemorrhagic stroke[1], meningitis, and so on. The clinician’s task is to determine which one it is so that the patient can be treated correctly. The differential diagnosis process involves administering diagnostic tests that are designed to either rule in or rule out conditions on the differential diagnosis list.
Returning to our example, the likelihood of concussion could be assessed by questioning the patient about any recent head or neck trauma (questions can be diagnostic tests!). If the patient denies such trauma (e.g., she has not played a contact sport, fallen, been in a motor vehicle accident, etc. in the last 24 hours), then we have probably ruled out concussion. The next task would be to rule out hemorrhagic stroke— strokes in young people are very rare but not unheard of, and the faster they are treated, the better the prognosis. We could rule out hemorrhagic stroke by looking for blood in the patient’s cerebrospinal fluid (the diagnostic test in that case is a spinal tap). Assuming that the patient’s spinal fluid is indeed clear of blood, we would then test to rule out meningitis. If that test is also clear, then we could safely assume that she has a migraine and offer treatment accordingly.
The order in which one rules in or rules out conditions on the differential diagnosis list depends on their relative severity, the costs associated with various tests, and the prevalence of the conditions in question. In this scenario, it was very important to quickly rule out stroke, because if it were a stroke, treatment would need to be initiated as soon as possible—whereas a migraine can wait an hour without causing further harm. This isn’t pleasant for the person with the migraine, but it won’t kill them or cause long-term disability. A brain tumor is also on the differential diagnosis list; however, that condition is very rare in patients in their 20s, and delaying treatment for a brain tumor by 24 hours would not matter (unlike for a stroke, which is also rare but for which one cannot delay treatment). Thus after ruling out concussion, meningitis, and stroke, we would treat the patient for a migraine. If she did not get better in 24–48 hours, we would return to the differential diagnosis list and possibly test for neuroblastoma or other brain cancers.
As mentioned above, often the same tests are used both for screening and for diagnostic testing; the distinction depends on context. If I do not have any symptoms of breast cancer and have a mammogram, then it is a screening test (screening is done in asymptomatic populations). If on the other hand I find a lump in my breast, go to the doctor, and she sends me for a mammogram, it is now a diagnostic test, because I am symptomatic.
Disease Critical Points and Other Things to Understand about Screening
The figures in this section and the idea of critical points are adapted from lectures given by Dr. David Slawson at the University of Virginia Medical System, Department of Family Medicine, in 2004-2005.
The natural course of a medical condition looks like this:

The first step is the biological onset of the disease. This could be the first mutation that turns the cell into a cancerous cell. It could be a virus getting in through someone’s mucous membranes and beginning to replicate. Importantly, biological onset is not observable.
Eventually, the person with the disease will have symptoms severe enough that they seek treatment: they go to a clinic, they go to the emergency room, they go to the pharmacy and buy some decongestant; they will eventually seek treatment of some kind. The exact timing will vary from person to person and from disease to disease.
The final stage in our natural history of disease is the outcome. Either they get better or they don’t.
So then what is screening? This is the idea of screening:

Remember that a screening program starts with asymptomatic people — normal, everyday people — and tests them to see if they have the disease.
The idea is to find the disease early. Screening is not primary prevention.[2] Screening finds early disease; it does not prevent the disease from occurring. Screening might well prevent poor outcomes from the disease (secondary prevention), but it doesn’t prevent the disease itself.
Thus the first criterion for a successful screening program is that a test exists that can detect early, pre-symptom disease. This is not always the case — for instance, we don’t screen for ovarian cancer partly because no such test exists at this time. A second criterion for a successful screening program is that the condition is prevalent enough and/or the costs of not treating it are high enough to make it worth screening for on a population level. Another reason we don’t screen for ovarian cancer is because the prevalence is very low, and thus a screening program would arguably not be worth the resources.
The next important idea is that every disease has a critical point. If you treat the disease before it gets to the critical point, you can make a difference in the outcome: the patient will be cured, will live longer, or will live better. However, if you treat the disease after the critical point, the treatment will have no effect (this is why we have hospice—after a certain point, further aggressive treatments are not useful and are potentially even harmful).
When thinking of implementing a screening program for a given disease, one must consider the timing of the critical points. For instance, what if the critical point (represented by the red line) for a given disease occurs here:

In the above scenario (Figure 11-3), it would not be cost-beneficial to screen for this condition, because detecting it early doesn’t help. By the time people seek help for their symptoms, there is still plenty of time to treat them. Screening in this scenario would not cause physical or emotional harm per se, but it would waste resources. We are learning that both prostate cancer and breast cancer probably fall into this category. Except for certain very high-risk groups, most men are no longer routinely screened for prostate cancer, and there is increasing evidence that mammograms might only be truly useful for high-risk women.ii
What if instead the critical point is here:

In this case (Figure 11-4), we also probably would not screen for this condition because by the time we screen, it’s already too late. Screening in this scenario would cause emotional harm because people would know that they have an untreatable disease for a longer period of time. For a highly contagious condition, however, we might screen people in this scenario—not so that we can treat them but so that they can take precautions and not spread it to others. Before we had antiretroviral drugs, for instance, we screened high-risk populations for HIV.
Screening, then, is most useful in this scenario:
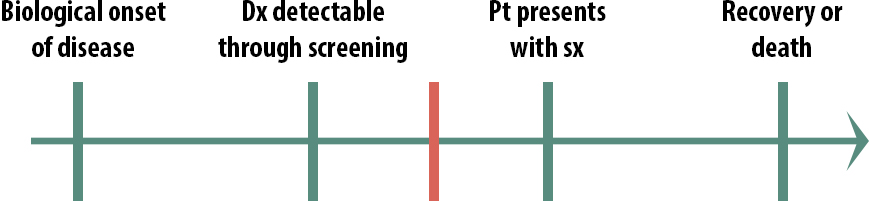
In this case, early detection does make a difference. By the time some patients present with symptoms, it is too late to treat them, but if we can detect the disease earlier than that, there is still time to help them. We still might not implement a population-wide screening program, if the disease is rare and the cost of the screening test quite high, for instance. But only in this scenario, where the critical point lies between screening detection and treatment seeking, should we even consider screening.
Accuracy of Screening and Diagnostic Tests
There are 4 test characteristics that we use to quantify how accurate a particular test is: sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV). The first 2 are known as “fixed test characteristics” because they do not change, regardless of disease prevalence. The PPV and NPV, however, do change when disease prevalence in the underlying population changes.
Calculation of these 4 test characteristics requires that we arrange our data in a 2 × 2 table. This time, however, instead of exposure on the left, we have the test result on the left:
| D+ | D- | Total | |
| T+ | TP | FP | TP+FP |
| T- | FN | TN | FN+TN |
| Total | TP+FN | FP+TN | TP+FP+TN+FN |
Looking at the screening 2 × 2 table, you’ll notice that the cells are no longer labeled ABCD. They still could be—and indeed, in many textbooks they are. However, I prefer this notation because it reminds you what each cell is in this scenario. Specifically, the top left cell contains “true positives”—these individuals do have the disease (according to a gold standard diagnosis method–see below) and tested positive using the screening or diagnostic test. The top right cell, on the other hand, contains “false positives”—people who tested positive using the screening or diagnostic test but do not actually have the disease. The bottom left cell contains the “false negatives”—these individuals have the disease but for some reason test negative. Finally, the bottom right cell is comprised of the “true negatives,” who do not have the disease and test negative.
One obtains data for a screening 2 × 2 table by administering both the test that we’re evaluating and a gold-standard diagnostic method to a large group of people. For example, the gold standard for diagnosing Alzheimer’s disease is the presence of a certain type of brain plaque, observable upon autopsy. Since this is not a feasible thing to do to living elderly patients who have suspected dementia, researchers developed the Mini Mental State (MMS) test.iii To create the above 2 × 2 table, then, one would administer the MMS to a group of elderly persons and categorize their results as either testing positive (T+) or testing negative (T−). Then one would collect autopsy data as they die and categorize those same individuals as either having had Alzheimer’s (D+) or not (D−).
In other scenarios, both can be done at the same time (rather than waiting for death)—for example, using the Beck Depression Inventory (BDI) as a test for depression and comparing results against a series of visits with a mental health professional qualified to definitively diagnose depression. The reason for having a test in the latter case is that the BDI is much quicker and cheaper than sending everyone for a formal psychiatric evaluation; the BDI is also a self-administered questionnaire, which can be utilized in large cohort studies (whereas the clinician-mediated diagnosis is untenable for large and/or geographically disparate study populations).
Note that one can calculate prevalence of the disease in the sample using a screening 2×2 table: everyone with disease (TP+FN) over everyone in the sample.
Sensitivity and Specificity
Sensitivity (Sn) is the probability that a patient tests positive given that they have the disease. In probability notation, this is written as follows:

Specificity (Sp) is the probability that a patient tests negative given that they do not have the disease:
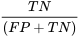
Both of these values are proportions and are usually expressed as percentages.
Recall that sensitivity and specificity are fixed test characteristics—they do not change if the prevalence of the condition in the sample changes. Sensitivity and specificity values are published when new tests become available, and are used by clinicians to decide what tests to order.
For diagnostic testing, recall that we are trying sometimes to rule in and other times to rule out. Two common mnemonic devices are SpIN and SnOUT: a test with high specificity, when positive, rules IN, and a test with high sensitivity, when negative, rules OUT. To understand why, look back at the formulae. The denominator for specificity is FP+TN (all the individuals without the disease), and the numerator is just TN. If the specificity is high (close to 100%), then FP must be very low. Thus a patient with a positive result on a highly specific test is probably a true positive. The same logic can be used to understand SnOUT: the denominator for sensitivity is TP+FN (all the individuals with the disease), and the numerator is just TP. If sensitivity is near 100%, then by definition there are few false negatives. A negative result on a highly sensitive test is thus almost certainly a true negative. Thus clinicians will choose a test with high sensitivity when they want to rule out (as in concussion or stroke, in our example above), and a test with high specificity when they want to rule in.
For screening purposes, we are testing an asymptomatic population—we thus want to minimize false negatives. This is because we wouldn’t want to tell someone that they are disease-free if they’re really not. Screening programs therefore utilize tests with high sensitivities.
Positive and Negative Predictive Values
The positive predictive value is the probability that you actually have the disease given that you tested positive (look carefully, and be sure you understand how this is different than sensitivity):

The negative predictive value is the probability that you do not have the disease given that you tested negative:

Again, these quantities are proportions and are usually expressed as percentages.
PPV and NPV are used to interpret test results once those results are known. Unlike sensitivity and specificity, however, PPV and NPV do change as the prevalence of disease in the sample changes—it is thus important to know something about the prevalence of disease in the target population to which an individual belongs before you can interpret their test results. For example, if a patient tests positive for tuberculosis (TB) and you know that the prevalence of TB in the population from which the patient comes is 10%, and the PPV given a 10% prevalence is 52.6%, then the interpretation of that test result is: there is a 52.6% chance that this patient has TB (there is thus a 47.4% chance that they do not have TB and the result was a false positive).
In general, PPV will decrease and NPV will increase as prevalence decreases. This makes intuitive sense: as a condition becomes more rare, then guessing that the patient does not have the disease becomes more and more likely to be correct. Extremely low PPV secondary to low prevalence was the rationale behind the 2009 recommendation by the US Preventive Services Task Force (USPSTF) that women in their 40s stop being screened for breast cancer unless they are extremely high-risk.iv The prevalence of disease among women in their 40s is very low (0.98%)v and the PPV in this population is thus well under 1%—this means that greater than 99% of women who are sent for follow-up testing (breast biopsy, usually) are false positives and thus undergo this expensive, invasive follow-up (with its corresponding emotional stress) unnecessarily. For women with a strong family history and/or who are known to be BRCA-1 or BRCA-2 carriers, mammography for 40-year-olds is still warranted—because these women come from an underlying population in which the prevalence (and thus the PPV) is much higher.
Example
Say a new test for anemia is developed that does not require a finger stick to obtain blood (no one likes needles!)—perhaps using a scanner that can detect hemoglobin levels through the thin skin on the underside of a wrist. The following 2 × 2 table is published:
| D+ | D- | Total | |
| T+ | 101 | 15 | 116 |
| T- | 18 | 866 | 884 |
| Total | 119 | 881 | 1000 |
In this case, the test results (either T+ or T-) would come from the wrist scanner, and the disease results (D+ or D-) would come from the usual method of diagnosing anemia, which requires a blood draw.
Sample Calculations
Using the data from the above table, we can calculate the four test characteristics.
Sensitivity =  = 84.9%
= 84.9%
Specificity = 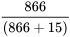 = 98.3%
= 98.3%
Positive Predictive Value = 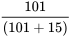 = 87.0%
= 87.0%
Negative Predictive Value = 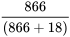 = 98.0%
= 98.0%
We can also calculate the prevalence of anemia in this sample.
Prevalence = 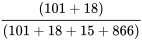 = 11.9%
= 11.9%
Let’s now say that there is a patient who took the new test and tested positive. However, we know that the patient is from a population with a lower prevalence of anemia than 11.9%—adolescent males, for example, in whom the prevalence is around 1%.vi In this case, the above PPV no longer applies. However, since we know the Sensitivity and Specificity, we can create a new 2 × 2 table, from which we can calculate a new PPV for a lower prevalence population. We begin by deciding (arbitrarily) that we will again have 1,000 people in the table:
| D+ | D- | total | |
| T+ | |||
| T- | |||
| total | 1000 |
If the prevalence is 1%, then 10 people would be expected to have the disease:
| D+ | D- | total | |
| T+ | |||
| T- | |||
| total | 10 | 990 | 1000 |
Since the sensitivity is 84.9%, and sensitivity is a fixed test characteristic, we can solve for true positives as follows:
Sn = 
0.849 = TP/10
TP = 8.49
We then subtract to get false negatives:
| D+ | D- | Total | |
| T+ | 8.49 | ||
| T- | 1.51 | ||
| Total | 10 | 990 | 1,000 |
We can do a similar calculation with the known specificity of 98.3%:
We can then fill in the nondiseased column:
| D+ | D- | Total | |
| T+ | 8.49 | 16.83 | 25.32 |
| T- | 1.51 | 973.17 | 974.68 |
| Total | 10 | 990 | 1,000 |
Now we can calculate our new PPV:
There is thus only a 33.5% chance that our male adolescent actually has anemia based on a positive skin scan test. (We would follow up with a blood draw to confirm—had he tested negative, the new NPV would have been 99.9%—no blood draw required!)
Summary
Screening and diagnostic testing are similar procedures; the difference depends on context (whether the tested person is symptomatic or not). Accuracy of such tests is quantified by sensitivity and specificity (used ahead of time to pick the correct test), and positive and negative predictive values (used after the test results are known, to interpret them). One must know the prevalence of a disease in the target population in order to use PPV and NPV.
References
i. Ring KL, Modesitt SC. Hereditary cancers in gynecology: what physicians should know about genetic testing, screening, and risk reduction. Obstet Gynecol Clin North Am. 2018;45(1):155-173. doi:10.1016/j.ogc.2017.10.011 (↵ Return)
ii. Welch HG, Prorok PC, Kramer BS. Breast-cancer tumor size and screening effectiveness. N Engl J Med. 2017;376(1):94-95. doi:10.1056/NEJMc1614282 (↵ Return)
iii. Rovner BW, Folstein MF. Mini-mental state exam in clinical practice. Hosp Pract Off Ed. 1987;22(1A):99, 103, 106, 110. (↵ Return)
iv. Final update summary: breast cancer, screening. US Preventive Services Task Force. https://www.uspreventiveservicestaskforce.org/Page/Document/UpdateSummaryFinal/breast-cancer-screening. Accessed November 27, 2018. (↵ Return)
v. USCS Data Visualizations. CDC. https://www.cdc.gov/cancer/dcpc/data/. Accessed November 27, 2018. (↵ Return)
vi. Looker AC, Dallman PR, Carroll MD, Gunter EW, Johnson CL. Prevalence of iron deficiency in the United States. JAMA. 1997;277(12):973-976. (↵ Return)
- There are two kinds of strokes: ischemic and hemorrhagic. Ischemic strokes are caused by blood clots in the brain, and hemorrhagic strokes are caused by bleeding in the brain. The latter are much more common in young people (ischemic strokes would be almost unheard of in an otherwise-healthy 24-year-old female), though ischemic strokes are more prevalent overall. These are really two different diseases, but they produce a very similar set of symptoms, so prior to our understanding the disease processes behind them, all such symptoms were classified as “stroke.” ↵
- This mistake regularly appears in the literature! See for instance Ring et al.i↵


