10.5: The Strengths of Acids and Bases
- Page ID
- 15283
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describe the difference between strong and weak acids and bases.
- Describe how a chemical reaction reaches chemical equilibrium.
- Define the pH scale and use it to describe acids and bases.
Acids and bases do not all demonstrate the same degree of chemical activity in solution. Different acids and bases have different strengths.
Strong and Weak Acids
Let us consider the strengths of acids first. A small number of acids ionize completely in aqueous solution. For example, when HCl dissolves in water, every molecule of HCl separates into a hydronium ion and a chloride ion:
\[\ce{HCl(g) + H2O(l) ->[\sim 100\%] H_3O^{+}(aq) + Cl^{-} (aq)} \label{Eq1} \]
HCl(aq) is one example of a strong acid, which is a compound that is essentially 100% ionized in aqueous solution. There are very few strong acids. The important ones are listed in Table \(\PageIndex{1}\).
| Acids | Bases |
|---|---|
| HCl | LiOH |
| HBr | NaOH |
| HI | KOH |
| HNO3 | Mg(OH)2 |
| H2SO4 | Ca(OH)2 |
| HClO4 |
By analogy, a strong base is a compound that is essentially 100% ionized in aqueous solution. As with acids, there are only a few strong bases, which are also listed in Table \(\PageIndex{1}\).
If an acid is not listed in Table \(\PageIndex{1}\), it is likely a weak acid, which is a compound that is not 100% ionized in aqueous solution. Similarly, a weak base is a compound that is not 100% ionized in aqueous solution. For example, acetic acid (\(\ce{HC2H3O2}\)) is a weak acid. The ionization reaction for acetic acid is as follows:
\[\ce{HC2H3O2(aq) + H2O(ℓ) \rightarrow H3O^{+}(aq) + C2H3O^{−}2(aq)} \label{Eq2} \]
Depending on the concentration of HC2H3O2, the ionization reaction may occur only for 1%–5% of the acetic acid molecules.
Many household products are acids or bases. For example, the owner of a swimming pool may use muriatic acid to clean the pool. Muriatic acid is another name for hydrochloric acid [\(\ce{HCl(aq)}\)]. Vinegar has already been mentioned as a dilute solution of acetic acid [\(\ce{HC2H3O2(aq)}\)]. In a medicine chest, one may find a bottle of vitamin C tablets; the chemical name of vitamin C is ascorbic acid (\(\ce{HC6H7O6}\)).
One of the more familiar household bases is ammonia (NH3), which is found in numerous cleaning products. As we mentioned previously, ammonia is a base because it increases the hydroxide ion concentration by reacting with water:
\[\ce{NH3(aq) + H2O(ℓ) \rightarrow NH^{+}4(aq) + OH^{−}(aq)} \label{Eq3} \]
Many soaps are also slightly basic because they contain compounds that act as Brønsted-Lowry bases, accepting protons from water and forming excess hydroxide ions. This is one reason that soap solutions are slippery.

Perhaps the most dangerous household chemical is the lye-based drain cleaner. Lye is a common name for sodium hydroxide, although it is also used as a synonym for potassium hydroxide. Lye is an extremely caustic chemical that can react with grease, hair, food particles, and other substances that may build up and form a clog in a pipe. Unfortunately, lye can also attack tissues and other substances in our bodies. Thus, when we use lye-based drain cleaners, we must be very careful not to touch any of the solid drain cleaner or spill the water it was poured into. Safer, nonlye drain cleaners use peroxide compounds to react on the materials in the clog and clear the drain.
Chemical Equilibrium in Weak Acids and Bases
The behavior of weak acids and bases illustrates a key concept in chemistry. Does the chemical reaction describing the ionization of a weak acid or base just stop when the acid or base is done ionizing? Actually, no. Rather, the reverse process—the reformation of the molecular form of the acid or base—occurs, ultimately at the same rate as the ionization process. For example, the ionization of the weak acid \(\ce{HC2H3O2 (aq)}\) is as follows:
\[\ce{HC2H3O2(aq) + H2O(ℓ) \rightarrow H3O^{+}(aq) + C2H3O^{−}2(aq)} \label{Eq4} \]
The reverse process also begins to occur:
\[\ce{H3O^{+}(aq) + C2H3O^{−}2(aq) \rightarrow HC2H3O2(aq) + H2O(ℓ)} \label{Eq5} \]
Eventually, there is a balance between the two opposing processes, and no additional change occurs. The chemical reaction is better represented at this point with a double arrow:
\[\ce{HC2H3O2(aq) + H2O(ℓ) <=> H3O^{+}(aq) + C2H3O^{-}2(aq)} \label{Eq6} \]
The \(\rightleftharpoons\) implies that both the forward and reverse reactions are occurring, and their effects cancel each other out. A process at this point is considered to be at chemical equilibrium (or equilibrium). It is important to note that the processes do not stop. They balance out each other so that there is no further net change; that is, chemical equilibrium is a dynamic equilibrium.
Write the equilibrium chemical equation for the partial ionization of each weak acid or base.
- HNO2(aq)
- C5H5N(aq)
Solution
- HNO2(aq) + H2O(ℓ) ⇆ NO2−(aq) + H3O+(aq)
- C5H5N(aq) + H2O(ℓ) ⇆ C5H5NH+(aq) + OH−(aq)
Write the equilibrium chemical equation for the partial ionization of each weak acid or base.
- \(HF_{(aq)}\)
- \(AgOH_{(aq)}\)
- CH3NH2(aq)
- Answer
-
a. HF(aq) + H2O(ℓ) ⇆ F−(aq) + H3O+(aq)
b. AgOH(aq) ⇆ Ag+(aq) + OH−(aq)
c. CH3NH2(aq) + H2O(ℓ) ⇆ CH3NH3+(aq) + OH−(aq)
Acid Ionization Constant, \(K_\text{a}\)
The ionization for a general weak acid, \(\ce{HA}\), can be written as follows:
\[\ce{HA} \left( aq \right) \rightleftharpoons \ce{H^+} \left( aq \right) + \ce{A^-} \left( aq \right) \nonumber \]
Because the acid is weak, an equilibrium expression can be written. An acid ionization constant \(\left( K_\text{a} \right)\) is the equilibrium constant for the ionization of an acid.
\[K_\text{a} = \frac{\left[ \ce{H^+} \right] \left[ \ce{A^-} \right]}{\left[ \ce{HA} \right]} \nonumber \]
The acid ionization represents the fraction of the original acid that has been ionized in solution. Therefore, the numerical value of \(K_\text{a}\) is a reflection of the strength of the acid. Weak acids with relatively higher \(K_\text{a}\) values are stronger than acids with relatively lower \(K_\text{a}\) values. Because strong acids are essentially \(100\%\) ionized, the concentration of the acid in the denominator is nearly zero and the \(K_\text{a}\) value approaches infinity. For this reason, \(K_\text{a}\) values are generally reported for weak acids only.
The table below is a listing of acid ionization constants for several acids. Note that polyprotic acids have a distinct ionization constant for each ionization step, with each successive ionization constant being smaller than the previous one.
| Name of Acid | Ionization Equation | \(K_\text{a}\) |
|---|---|---|
| Sulfuric acid |
\(\ce{H_2SO_4} \rightleftharpoons \ce{H^+} + \ce{HSO_4^-}\) \(\ce{HSO_4} \rightleftharpoons \ce{H^+} + \ce{SO_4^{2-}}\) |
very large \(1.3 \times 10^{-2}\) |
| Hydrofluoric acid | \(\ce{HF} \rightleftharpoons \ce{H^+} + \ce{F^-}\) | \(7.1 \times 10^{-4}\) |
| Nitrous acid | \(\ce{HNO_2} \rightleftharpoons \ce{H^+} + \ce{NO_2^-}\) | \(4.5 \times 10^{-4}\) |
| Benzoic acid | \(\ce{C_6H_5COOH} \rightleftharpoons \ce{H^+} + \ce{C_6H_5COO^-}\) | \(6.5 \times 10^{-5}\) |
| Acetic acid | \(\ce{CH_3COOH} \rightleftharpoons \ce{H^+} + \ce{CH_3COO^-}\) | \(1.8 \times 10^{-5}\) |
| Carbonic acid |
\(\ce{H_2CO_3} \rightleftharpoons \ce{H^+} + \ce{HCO_3^-}\) \(\ce{HCO_3^-} \rightleftharpoons \ce{H^+} + \ce{CO_3^{2-}}\) |
\(4.2 \times 10^{-7}\) \(4.8 \times 10^{-11}\) |
Hydrofluoric acid \(HF_{(aq)}\) reacts directly with glass (very few chemicals react with glass). Hydrofluoric acid is used in glass etching.
Strong and Weak Bases and Base Ionization Constant, Kb
As with acids, bases can either be strong or weak, depending on their extent of ionization. A strong base is a base, which ionizes completely in an aqueous solution. The most common strong bases are soluble metal hydroxide compounds such as potassium hydroxide. Some metal hydroxides are not as strong simply because they are not as soluble. Calcium hydroxide is only slightly soluble in water, but the portion that does dissolve also dissociates into ions.
A weak base is a base that ionizes only slightly in an aqueous solution. Recall that a base can be defined as a substance, which accepts a hydrogen ion from another substance. When a weak base such as ammonia is dissolved in water, it accepts an \(\ce{H^+}\) ion from water, forming the hydroxide ion and the conjugate acid of the base, the ammonium ion.
\[\ce{NH_3} \left( aq \right) + \ce{H_2O} \left( l \right) \rightleftharpoons \ce{NH_4^+} \left( aq \right) + \ce{OH^-} \left( aq \right) \nonumber \]
The equilibrium greatly favors the reactants and the extent of ionization of the ammonia molecule is very small.
An equilibrium expression can be written for the reactions of weak bases with water. Because the concentration of water is extremely large and virtually constant, the water is not included in the expression. A base ionization constant \(\left( K_\text{b} \right)\) is the equilibrium constant for the ionization of a base. For ammonia the expression is:
\[K_\text{b} = \frac{\left[ \ce{NH_4^+} \right] \left[ \ce{OH^-} \right]}{\left[ \ce{NH_3} \right]} \nonumber \]
The numerical value of \(K_\text{b}\) is a reflection of the strength of the base. Weak bases with relatively higher \(K_\text{b}\) values are stronger than bases with relatively lower \(K_\text{b}\) values. Table \(\PageIndex{3}\) is a listing of base ionization constants for several weak bases.
| Name of Base | Ionization Equation | \(K_\text{b}\) |
|---|---|---|
| Methylamine | \(\ce{CH_3NH_2} + \ce{H_2O} \rightleftharpoons \ce{CH_3NH_3^+} + \ce{OH^-}\) | \(5.6 \times 10^{-4}\) |
| Ammonia | \(\ce{NH_3} + \ce{H_2O} \rightleftharpoons \ce{NH_4^+} + \ce{OH^-}\) | \(1.8 \times 10^{-5}\) |
| Pyridine | \(\ce{C_5H_5N} + \ce{H_2O} \rightleftharpoons \ce{C_5H_5NH^+} + \ce{OH^-}\) | \(1.7 \times 10^{-9}\) |
| Acetate ion | \(\ce{CH_3COO^-} + \ce{H_2O} \rightleftharpoons \ce{CH_3COOH} + \ce{OH^-}\) | \(5.6 \times 10^{-10}\) |
| Fluoride ion | \(\ce{F^-} + \ce{H_2O} \rightleftharpoons \ce{HF} + \ce{OH^-}\) | \(1.4 \times 10^{-11}\) |
| Urea | \(\ce{H_2NCONH_2} + \ce{H_2O} \rightleftharpoons \ce{H_2NCONH_3^+} + \ce{OH^-}\) | \(1.5 \times 10^{-14}\) |
The Ion-Product of Water
As we have already seen, H2O can act as an acid or a base. Within any given sample of water, some \(\ce{H2O}\) molecules are acting as acids, and other \(\ce{H2O}\) molecules are acting as bases. The chemical equation is as follows:
\[\color{red}{\underbrace{\ce{H2O}}_{\text{acid}}} + \color{blue}{\underbrace{\ce{H2O}}_{\text{base}}} \color{black} \ce{<=> H3O^{+} + OH^{−}} \label{Auto} \]
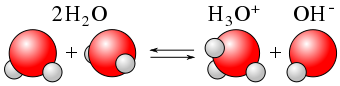 Figure \(\PageIndex{2}\): Autoionization of water, giving hydroxide and hydronium ions.
Figure \(\PageIndex{2}\): Autoionization of water, giving hydroxide and hydronium ions.
Similar to a weak acid, the autoionization of water is an equilibrium process, and is more properly written as follows:
\[\ce{H2O(ℓ) + H2O(ℓ) <=> H3O^{+}(aq) + OH^{-}(aq)} \label{Eq7} \]
We often use the simplified form of the reaction:
\[\ce{H2O(l) <=> H+(aq) + OH−(aq)} \nonumber \]
The equilibrium constant for the autoionization of water is referred to as the ion-product for water and is given the symbol Kw.
\[K_w = [\ce{H^{+}}][\ce{OH^{-}}] \nonumber \]
The ion-product of water (Kw) is the mathematical product of the concentration of hydrogen ions and hydroxide ions. Note that H2O is not included in the ion-product expression because it is a pure liquid. The value of Kw is very small, in accordance with a reaction that favors the reactants. At 25oC, the experimentally determined value of \(K_w\) in pure water is 1.0×10−14.
\[K_w = [\ce{H^{+}}][\ce{OH^{−}}] = 1.0 \times 10^{−14} \nonumber \]
In a sample of pure water, the concentrations of hydrogen and hydroxide ions are equal to one another. Pure water or any other aqueous solution in which this ratio holds is said to be neutral. To find the molarity of each ion, the square root of Kw is taken.
[H+] = [OH−] = 1.0×10−7
The product of these two concentrations is 1.0×10−14
\[\color{red}{\ce{[H^{+}]}} \color{black}{\times} \color{blue}{\ce{[OH^{-}]}} \color{black} = (1.0 \times 10^{-7})( 1.0 \times 10^{-7}) = 1.0 \times 10^{-14} \nonumber \]
- For acids, the concentration of H+ or [H+]) is greater than 1.0×10−7 M
- For bases, the concentration of OH− or [OH−] is greater than 1.0×10−7 M.
Aqueous HCl is an example of acidic solution. Hydrogen chloride (HCl) ionizes to produce H+ and Cl− ions upon dissolving in water. This increases the concentration of H+ ions in the solution. According to Le Chatelier's principle, the equilibrium represented by
\[\ce{H2O(l) <=> H^{+}(aq) + OH^{−}(aq)} \nonumber \]
\[\ce{HCl(g) -> H^{+}(aq) + Cl^{−}(aq)} \nonumber \]
is forced to the left, towards the reactant. As a result, the concentration of the hydroxide ion decreases.
Now, consider KOH (aq), a basic solution. Solid potassium hydroxide (KOH) dissociates in water to yield potassium ions and hydroxide ions.
KOH(s) → K+(aq) + OH−(aq)
The increase in concentration of the OH− ions will cause a decrease in the concentration of the H+ ions.
No matter whether the aqueous solution is an acid, a base, or neutral:and the ion-product of [H+][OH−] remains constant.
- For acidic solutions, [H+]) is greater than [OH−].
- For basic solutions, [OH−] is greater than [H+].
- For neutral solutions, [H3O+] = [OH−] = 1.0×10−7M
This means that if you know \(\ce{[H^{+}]}\) for a solution, you can calculate what \(\ce{[OH^{−}]}\)) has to be for the product to equal \(1.0 \times 10^{−14}\), or if you know \(\ce{[OH^{−}]}\)), you can calculate \(\ce{[H^{+}]}\). This also implies that as one concentration goes up, the other must go down to compensate so that their product always equals the value of \(K_w\).
\[K_w = \color{red}{\ce{[H_3O^+]}} \color{blue}{\ce{[OH^{-}]}} \color{black} = 1.0 \times 10^{-14} \label{eq10} \]
Hydrochloric acid (HCl) is a strong acid, meaning it is 100% ionized in solution. What is the [H+] and the [OH−] in a solution of 2.0×10−3 M HCl?
Solution
Step 1: List the known values and plan the problem.
Known
- [HCl] = 2.0×10−3 M
- Kw = 1.0×10−14
Unknown
- [H+]=?M
- [OH−]=?M
Because HCl is 100% ionized, the concentration of H+ ions in solution will be equal to the original concentration of HCl. Each HCl molecule that was originally present ionizes into one H+ ion and one Cl− ion. The concentration of OH− can then be determined from the [H+] and Kw.
Step 2: Solve.
[H+]=2.0×10−3 M
Kw = [H+][OH−] = 1.0×10−14
[OH−] = Kw/[H+] = 1.0×10−14/2.0×10−3 = 5.0×10−12 M
Step 3: Think about your result.
The [H+] is much higher than the [OH−] because the solution is acidic. As with other equilibrium constants, the unit for Kw is customarily omitted.
Exercise \(\PageIndex{2}\)
Sodium hydroxide (NaOH) is a strong base. What is the [H+] and the [OH−] in a 0.001 M NaOH solution at 25 °C?
- Answer
-
[OH−] = 0.001M or 1 x 10-3M; [H+]=1×10−11M.
The pH Scale
One qualitative measure of the strength of an acid or a base solution is the pH scale, which is based on the concentration of the hydronium (or hydrogen) ion in aqueous solution.
\[pH = -\log[H^+] \nonumber \]
or
\[pH = -\log[H_3O^+] \nonumber \]
Figure \(\PageIndex{3}\) illustrates this relationship, along with some examples of various solutions. Because hydrogen ion concentrations are generally less than one (for example \(1.3 \times 10^{-3}\,M\)), the log of the number will be a negative number. To make pH even easier to work with, pH is defined as the negative log of \([H_3O^+]\), which will give a positive value for pH.
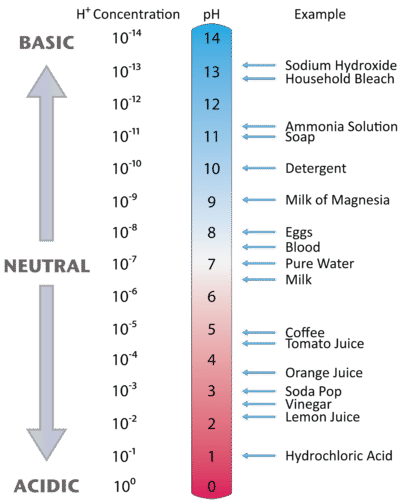 Figure \(\PageIndex{3}\): The relationaship between [H+] and \(pH\) values for several common materials.
Figure \(\PageIndex{3}\): The relationaship between [H+] and \(pH\) values for several common materials.
A neutral (neither acidic nor basic) solution has a pH of 7. A pH below 7 means that a solution is acidic, with lower values of pH corresponding to increasingly acidic solutions. A pH greater than 7 indicates a basic solution, with higher values of pH corresponding to increasingly basic solutions. Thus, given the pH of several solutions, you can state which ones are acidic, which ones are basic, and which are more acidic or basic than others. These are summarized in Table \(\PageIndex{4}.
Table \(\PageIndex{4}\): Acidic, Basic and Neutral pH Values
| Classification | Relative Ion Concentrations | pH at 25 °C |
|---|---|---|
| acidic | [H+] > [OH−] | pH < 7 |
| neutral | [H+] = [OH−] | pH = 7 |
| basic | [H+] < [OH−] | pH > 7 |
Find the pH, given the \([H^+]\) of the following:
- 1 ×10-3 M
- 2.5 ×10-11 M
- 4.7 ×10-9 M
Solution
pH = - log [H3O+]
Substitute the known quantity into the equation and solve. Use a scientific calculator for b and c.
- pH = - log [1 × 10−3 ] = 3.0 (1 decimal place since 1 has 1 significant figure)
- pH = - log [2.5 ×10-11] = 10.60 (2 decimal places since 2.5 has 2 significant figures)
- pH = - log [4.7 ×10-9] = 8.33 (2 decimal places since 4.7 has 2 significant figures)
Note on significant figures:
Because the number(s) before the decimal point in the pH value relate to the power on 10, the number of digits after the decimal point (underlined) is what determines the number of significant figures in the final answer.
Exercise \(\PageIndex{3}\)
Find the pH, given[H+] of the following:
- 5.8 ×10-4 M
- 1.0×10-7 M
- Answer
-
a. 3.24
b. 7.00
Table \(\PageIndex{5}\) lists the pH of several common solutions. The most acidic among the listed solutions is battery acid with the lowest pH value (0.3). The most basic is 1M NaOH solution with the highest pH value of 14.0. Notice that some biological fluids (stomach acid and urine) are nowhere near neutral. You may also notice that many food products are slightly acidic. They are acidic because they contain solutions of weak acids. If the acid components of these foods were strong acids, the food would likely be inedible.
| Solution | pH |
|---|---|
| battery acid | 0.3 |
| stomach acid | 1–2 |
| lemon or lime juice | 2.1 |
| vinegar | 2.8–3.0 |
| Coca-Cola | 3 |
| wine | 2.8–3.8 |
| beer | 4–5 |
| coffee | 5 |
| milk | 6 |
| urine | 6 |
| pure H2O | 7 |
| (human) blood | 7.3–7.5 |
| sea water | 8 |
| antacid (milk of magnesia) | 10.5 |
| NH3 (1 M) | 11.6 |
| bleach | 12.6 |
| NaOH (1 M) | 14.0 |
Label each solution as acidic, basic, or neutral based only on the stated \(pH\).
- milk of magnesia, pH = 10.5
- pure water, pH = 7
- wine, pH = 3.0
Solution
- With a pH greater than 7, milk of magnesia is basic. (Milk of magnesia is largely Mg(OH)2.)
- Pure water, with a pH of 7, is neutral.
- With a pH of less than 7, wine is acidic.
Exercise \(\PageIndex{4}\)
Identify each substance as acidic, basic, or neutral based only on the stated \(pH\).
- human blood with \(pH\) = 7.4
- household ammonia with \(pH\) = 11.0
- cherries with \(pH\) = 3.6
- Answer
-
a. slightly basic
b. basic
c. acidic
Acid Rain
Normal rainwater has a pH between 5 and 6 due to the presence of dissolved CO2 which forms carbonic acid:
\[\ce{H2O (l) + CO2(g) ⟶ H2CO3(aq)} \label{14} \]
\[\ce{H2CO3(aq) \rightleftharpoons H^+(aq) + HCO3^- (aq)} \label{15} \]
Acid rain is rainwater that has a pH of less than 5, due to a variety of nonmetal oxides, including CO2, SO2, SO3, NO, and NO2 being dissolved in the water and reacting with it to form not only carbonic acid, but sulfuric acid and nitric acid. The formation and subsequent ionization of sulfuric acid are shown here:
\[\ce{H2O (l) + SO3(g) ⟶ H2SO4(aq)} \label{16} \]
\[\ce{H2SO4(aq) ⟶ H^+(aq) + HSO4^- (aq)} \label{17} \]
Carbon dioxide is naturally present in the atmosphere because we and most other organisms produce it as a waste product of metabolism. Carbon dioxide is also formed when fires release carbon stored in vegetation or when we burn wood or fossil fuels. Sulfur trioxide in the atmosphere is naturally produced by volcanic activity, but it also stems from burning fossil fuels, which have traces of sulfur, and from the process of “roasting” ores of metal sulfides in metal-refining processes. Oxides of nitrogen are formed in internal combustion engines where the high temperatures make it possible for the nitrogen and oxygen in air to chemically combine.
Acid rain is a particular problem in industrial areas where the products of combustion and smelting are released into the air without being stripped of sulfur and nitrogen oxides. In North America and Europe until the 1980s, it was responsible for the destruction of forests and freshwater lakes, when the acidity of the rain actually killed trees, damaged soil, and made lakes uninhabitable for all but the most acid-tolerant species. Acid rain also corrodes statuary and building facades that are made of marble and limestone (Figure \(\PageIndex{4}\)). Regulations limiting the amount of sulfur and nitrogen oxides that can be released into the atmosphere by industry and automobiles have reduced the severity of acid damage to both natural and manmade environments in North America and Europe. It is now a growing problem in industrial areas of China and India.
 Figure \(\PageIndex{4}\): (a) Acid rain makes trees more susceptible to drought and insect infestation, and depletes nutrients in the soil. (b) It also is corrodes statues that are carved from marble or limestone. (credit a: modification of work by Chris M Morris; credit b: modification of work by “Eden, Janine and Jim”/Flickr)
Two photos are shown. Photograph a on the left shows the upper portion of trees against a bright blue sky. The tops of several trees at the center of the photograph have bare branches and appear to be dead. Image b shows a statue of a man that appears to from the revolutionary war era in either marble or limestone.
Figure \(\PageIndex{4}\): (a) Acid rain makes trees more susceptible to drought and insect infestation, and depletes nutrients in the soil. (b) It also is corrodes statues that are carved from marble or limestone. (credit a: modification of work by Chris M Morris; credit b: modification of work by “Eden, Janine and Jim”/Flickr)
Two photos are shown. Photograph a on the left shows the upper portion of trees against a bright blue sky. The tops of several trees at the center of the photograph have bare branches and appear to be dead. Image b shows a statue of a man that appears to from the revolutionary war era in either marble or limestone.
Key Takeaways
- Acids and bases can be strong or weak depending on the extent of ionization in solution.
- Most chemical reactions reach equilibrium at which point there is no net change.
- The ion-product of [H+][OH−] in an aqueous solution remains constant.
- A pH value is simply the negative of the logarithm of the H+ ion concentration (-log[H+]).
- The pH scale is used to succinctly communicate the acidity or basicity of a solution.
- A solution is acidic if pH < 7.
- A solution is basic if pH > 7.
- A solution is neutral if pH = 7.

