1.6: Bias

Learning Objectives

After reading this chapter, you will be able to do the following:

1. Define bias, and differentiate it from random error
2. Differentiate between the different types of bias common to epidemiologic studies, and provide illustrative examples of each

As we learned in the previous chapter, random error exists in all studies, because it exists to some degree in all measurements. Standard statistical methods are used to quantify random error and the role it may or may not have played in the interpretation of a study’s results. Random errors cannot be eliminated entirely, and by correctly interpreting p-values and confidence intervals (CIs), we can place our results in the appropriate context.

Bias, on the other hand, refers to systematic errors, meaning that they disproportionately affect the data in one direction only—so, for example, we would always underestimate or always overestimate when cutting the 6 tablespoons of butter for our cake (see chapter 5). There are many potential sources of bias in epidemiologic studies; here we will cover some of the most common. As with random error, all studies contain some degree of bias, and like with random error, we do our best to minimize it. The difference is that statistical methods cannot help us with bias.

Bias results in a calculated measure of association that is either above or below what it “should” be, because our data were skewed in one direction or the other. It is impossible to know the magnitude of the bias or even the direction. Did we over- or underestimate the risk ratio (RR)? By how much? We will never know the answers to these questions, but by thinking through likely directions of systematic errors (e.g., people will typically overestimate how much exercise they get), we can often make educated guesses about the direction of a bias and perhaps also its magnitude. But they are only guesses.

Bias can be minimized with correct study design and measurement techniques, but it can never be omitted entirely. All studies have bias because humans are involved, and humans are inherently biased.ⁱ Good scientists will ponder potential sources of bias during study planning phases, working to minimize them. They will also make an honest appraisal of residual bias at the end of a study and discuss this in the limitations section of a paper’s discussion section (see appendix 1).

Internal versus External Validity

Bias can affect both the internal validity and the external validity of a study. The former is a much more serious issue. Internal validity refers to the inner workings of a study: Was the best design used? Were variables measured in a reasonable way? Did the authors conduct the correct set of analyses? Note that although we can’t measure or quantify internal validity, an understanding of epidemiology and biostatistics allows for a qualitative appraisal. We can believe the results of a study that appears to be internally valid. A study that has major methodologic issues, however, lacks internal validity, and we probably should not accept the results.

If a study lacks internal validity, stop. There is rarely a need to assess it further. On the other hand, if a study does seem to have internal validity, we then assess external validity, or generalizability. External validity refers to how well the results of this particular study could be applied to the larger population. Recall from chapter 1 that the target population is the group about whom we wish to say something, using data collected from our sample. Occasionally, we find a study that is internally valid—meaning, it was conducted in an entirely correct way—but for some reason, the sample is not sufficiently representative of the target population. For example, during my dissertation work, I used cohort data to estimate the effects of maternal physical activity during pregnancy on various birth outcomes.ⁱⁱ The data came from a large pregnancy cohort and included data on hundreds of exposures and dozens of outcomes.ⁱⁱⁱ The inclusion criteria were lenient—all women pregnant with a singleton fetus planning to deliver at a certain hospital were eligible. Much like we find in the general population, the pregnant people in this cohort were mostly sedentary.^ii,iv

In some more recent work, I was looking specifically at physical activity during pregnancy as the only exposure; thus, my advertisement to recruit women into the study mentioned that I was studying exercise in pregnancy (rather than pregnancy in general).^[1] In this more recent study, I had very few sedentary people—indeed, I have a few who reported running half marathons while pregnant! Since this is not normal, my study—though it does have reasonable internal validity—cannot be generalized to all pregnant women but only to the subpopulation of them who get a fair bit of physical activity. It lacks external validity. Because it has good internal validity, I can generalize the results to highly active pregnant women—just not to all pregnant women.

Representativeness of Samples

If you have a sample that is not representative of the underlying population, this affects external validity. The extent to which this is a concern, though, depends on the research question. Questions that apply mainly to biology (e.g., do statins lower serum cholesterol levels?) do not necessarily require representative samples, because physiology does not usually vary to any great extent between people with different demographic characteristics (differences by sex are the one exception): my body likely processes statin drugs in a nearly-identical manner to that of most other women’s. However, when the research question involves behavior, then we must be very concerned about representativeness, because behavior varies greatly by demographics and social context. Thus, “Do statins lower serum cholesterol levels?” is a very different question than “If you prescribe statins for people with high cholesterol, will they live longer?” since the latter requires behavior on both the clinician’s part (providing the prescription) and the patient’s part (filling the prescription and then taking the medication as directed).

Figure 6-1 illustrates the difference between internal validity and external validity. This uses the cohort diagram, but the same principle applies to all study designs:

Figure 6-1

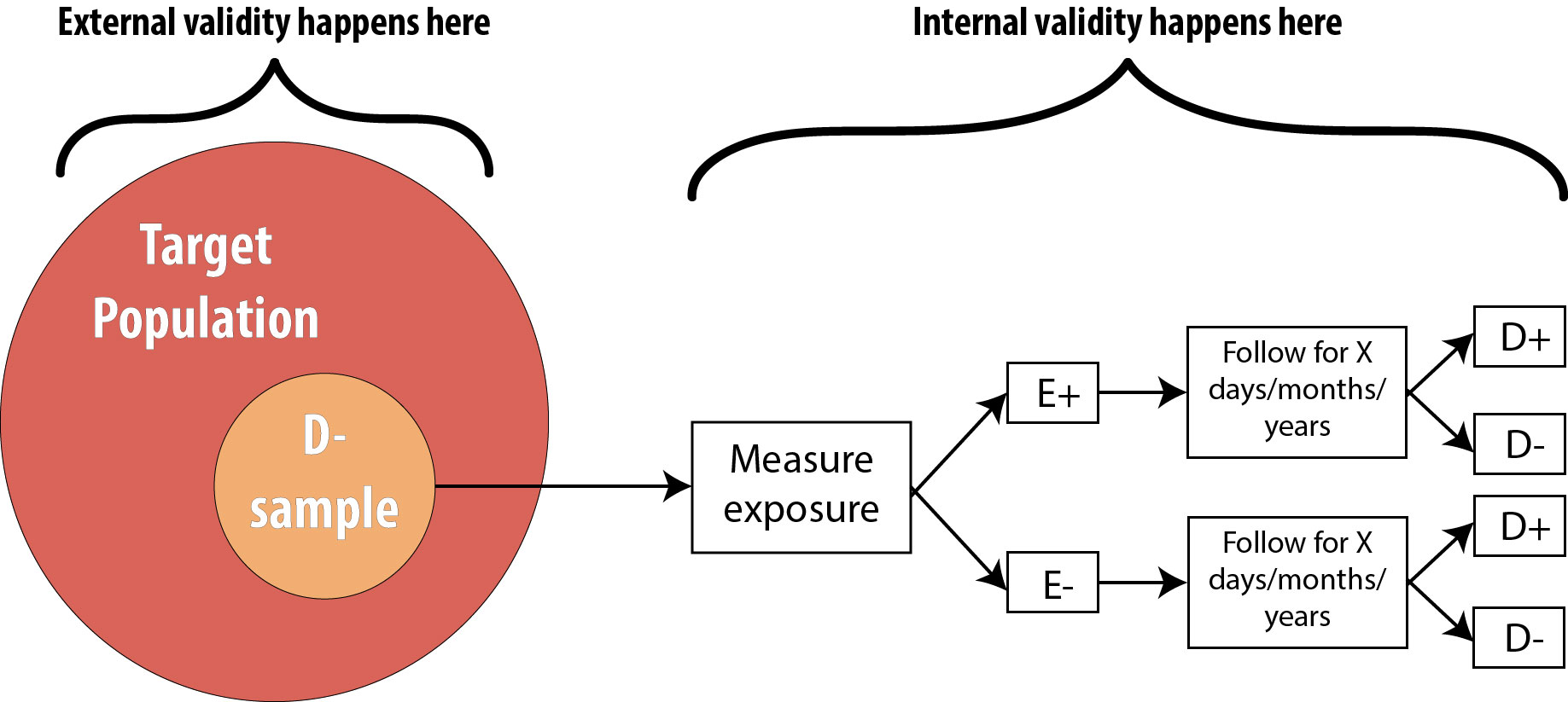
Selection Bias

Selection bias can affect either the internal or the external validity of a study. The above example about exercise in pregnancy (where I had a non-representative sample from the population) is the kind of selection bias affecting external validity: my results are generalizable only to the subset of the population from whom my sample actually was drawn rather than to the entire population. This sort of selection bias is not ideal, but one can easily recover by simply narrowing the target population to whom the results will apply. Asking “Who did the researchers get? Who did they miss?” will help in assessing the extent of overall selection bias.

In other cases, selection bias can affect internal validity. This is much worse, since the results of that study cannot be applied to anyone, because it has fundamental flaws. Selection bias adversely affecting internal validity occurs when the exposed and unexposed groups (for a cohort study) or the diseased and nondiseased groups (for a case-control study) are not drawn from the same population. For example, in a study of maternal physical activity and labor outcomes,^vi the “active” group was recruited from a prenatal exercise class, but the “sedentary” group was recruited from prenatal care clinics. To the extent that people who voluntarily choose to pay for and attend an exercise class specifically for pregnant women are different than the overall group of women getting prenatal care, this study has a selection bias affecting internal validity, because the exposed and unexposed groups (samples) come from different populations. Again, asking, “Who did they get? Who did they miss?” and also “Was this different between the two groups?” will help here.

Selection bias affecting internal validity can creep up in other, less obvious ways, mostly relating to missing data. Was the participation rate different between the 2 groups? Was there more loss to follow-up in one group versus the other? Either of these could lead to groups that might not reflect the same underlying population, since the kinds of people who agree to participate in studies are different than those who don’t, and the kinds of people who drop out are different than those who don’t. For instance, in studies of older adults, the sickest patients tend to drop out because they become too sick to attend the study-related clinic visits. If this occurs more in one study group than the other, it leads to selection bias.

Healthy worker bias is a type of selection bias, and it refers to the fact that people who can work are generally healthier than the overall population because the overall population includes people who are too sick to work. Thus studies that recruit from a population of people who work may lack external generalizability—which is fine, as long as one is careful when applying the study’s results. However, healthy worker bias can also affect internal validity if one group is recruited specifically from a population of workers and the other from the general population. For instance, if we suspect that Factory A has an environmental toxin (and our cohort study’s exposed group consists of workers from Factory A), then our unexposed group needs to be workers from somewhere else—not, say, spouses or neighbors (who may or may not work) of the exposed participants.

Misclassification Bias

Misclassification refers simply to measuring things incorrectly, such that study participants get put into the wrong box in the 2 x 2 table: we call them “diseased” when really they’re not (or vice versa); we call them “exposed” when really they’re not (or vice versa).

Continuing with our exercise in pregnancy example, say we recruit 1,000 pregnant women and assess their levels of physical activity. We decide that anyone meeting the recommendation for physical activity during pregnancy (30 minutes of moderate activity, most days of the week^vii[2]) will be classified as “exposed,” and anyone reporting less activity will be “unexposed.” In general, all people will over-report their levels of physical activity.^ix(p46) Thus in our study of 1,000 women, we would expect some level of misclassification—if everyone slightly overreports their amount of physical activity, then those people who actually got just under the recommended amount will be incorrectly classified because their over-reporting will bump them up into the exposed (met the guidelines) group.

If this is what the data should look like (imagine any disease you like here):

	D+	D-
E+	200	100
E-	300	400

But instead, if we incorrectly classify some women as exposed because of overreporting, the table might look like this:

	D+	D-
E+	230	140
E-	270	360

This is called nondifferential misclassification, because it occurs at the same rate (here, 10% of unexposed were incorrectly classified as exposed) in both the diseased and nondiseased groups. Nondifferential misclassification is not quite the same as random error—in random error, we might have 10% misclassification, but it would go in both directions. Here we really only expect overreporting of physical activity, so it is a systematic error, or bias. Misclassification, like all other forms of bias, affects studies by giving us the wrong estimate of association.

Example \(\PageIndex{1}\): Misclassification

Using the first 2 x 2 table above (ie, the “correct” data—note that this is almost never observable), the odds ratio (OR) is:

\[\mathrm{OR}=\frac{200 \times 400}{300 \times 100}=2.67\]

Whereas the odds ratio for the biased data (the ones we actually collected in our study) is:

\[\mathrm{OR}=\frac{230 \times 360}{140 \times 270}=2.19\]

The result of the calculation with data including nondifferential misclassification is closer to the null than the correct one would be. In real life, we cannot ever observe the “correct” table, and thus we cannot know by how much or in which direction our estimate is biased—just that it is.

Nondifferential Misclassification: Bias towards the Null?

In the exercise in pregnancy example, the OR estimate based on the biased data was biased toward the null (i.e., it’s closer to 1.0, the null value for odds ratios), but it could just as easily have been biased away from the null. Some older epidemiology textbooks will say that nondifferential misclassification always biases toward the null, but it turns out that this is not true.^9p143 It’s best to assume that you don’t know which way the bias is going.

On the plus side, even if the data are misclassified, as long as it’s nondifferential misclassification, we have probably still ranked people correctly. If everyone overestimates their physical activity, we can still tell the couch potatoes from the marathon runners. Thus, although the estimate of association we calculated with our misclassified data (in which everyone added, say, 30–60 minutes to their weekly exercise totals) is almost certainly not “correct,” with nondifferential misclassification, we can often still say something about the results (perhaps that the more exercise one gets, the lower one’s risk of heart disease?). This statement will almost certainly remain true, even if we were able to correct for the overestimate of everyone’s physical activity and generate an unbiased estimate of association.

The flip side is differential misclassification. With differential misclassification, we again find that some people are put into the wrong boxes in the 2 × 2 table, but this time it is not equally distributed across all study groups. Perhaps diseased people misreport more than nondiseased people. Or perhaps investigators are subconsciously more likely to classify someone as “diseased” if they are known to be exposed. Differential misclassification is considered a fatal threat to a study’s internal validity. Study authors, knowing this, will often acknowledge measurement errors in their study but claim that they are nondifferential and therefore essentially irrelevant. When you encounter such claims, think it through for yourself, and be sure you agree with the authors before citing their work. Differential misclassification is more common than many of us would like to admit.

Misclassification goes by numerous other names, including social desirability bias, interviewer bias, clinician bias, recall bias, and so on. Regardless of name, however, misclassification boils down to people being called exposed when they’re not, not exposed when they are, not diseased when really they are, or diseased when really they’re not. When considering self-reported data, as discussed in the previous chapter, you must first ask yourself, “Can people tell me this?” If not, stop. But if yes, then you must consider, “Will people tell me this?” If not, then the data may have bias from misclassification.

Sensitivity Analyses

Sometimes called bias analysis, a sensitivity analysis is a set of extra analyses conducted after the main results of a study are known, with the goal of quantifying how much bias there might have been and in which direction it shifted the results. Not all research questions and datasets are amenable to sensitivity analysis, but for those that are, it’s a great way for authors to increase the perceived validity of their results. There is no set way of conducting a sensitivity analysis; rather, one examines all assumptions made as part of an analysis and tests the extent to which those assumptions, rather than an underlying true association, drove the results.

For example, if we were studying physical activity, and in our main analysis decided that anyone meeting the guidelines was “active” and all other people in the study were “sedentary,” then one sensitivity analysis might change this cutoff point (perhaps now we declare that anyone accumulating 2 or more hours per week of exercise is “active,” even though this is less than the guidelines suggest) and see what the new estimate of association is. If the new estimate is close to the original one, then we can conclude that our choice of cutoff point (an assumption we made during analysis) did not affect the results extensively. This alone does not preclude the possibility that the original results are incorrect, but it does lessen the possibility that we would find a vastly different answer if we repeated the study using slightly different methods.

Missing data on individual variables also leads to misclassification—for instance, in the US, people do not like to talk about money, so often questions on income go unanswered. If the kind of person who leaves the income question blank is different than the kind of person who answers it, then the data are not missing at random. If data truly are missing at random (which might happen if, for instance, some people genuinely don’t see the question because of a quirk in the page layout), then the result is a slightly smaller sample size (and correspondingly less power), but otherwise this has no adverse effects. However, in real life, data are almost never missing at random, which means they are missing according to some pattern—and thus are creating a bias. If study authors claim that they have data missing at random, think carefully about the scenario and make sure you agree. More often, study authors simply don’t mention missing data at all.^[3] If an important variable in the analysis is missing for more than 5% of the sample, yet this is not discussed by the authors, then be wary of the results. They are probably biased.

Publication Bias

Publication bias arises because papers with more exciting results are more likely to get published. A paper whose main finding is “there is no association between x and y” is difficult to get published—so much so that there is an entire, legitimate, peer-reviewed journal dedicated solely to publishing these so-called negative results.

This type of bias does not apply to individual studies, but rather to areas of the literature as a whole. If papers with larger estimates of association and/or smaller p-values are more likely to get published, then when you attempt to look at the entire body of literature on a given topic (e.g., should elderly people take prophylactic aspirin to prevent heart attacks?), the picture you get is biased, because only the exciting papers were published. All the papers that showed no effect of aspirin on heart attack were not published. This is worth keeping in mind whenever you are doing literature searches and is discussed further in chapter 9.

Conclusion

All epidemiologic studies include bias. Investigators can minimize the biases that are present through good design and measurement methods, but some will always remain. Those biases affecting a study’s internal validity (selection bias that pertains more to one group than another, or differential misclassification) render that study either entirely useless or useful only with extreme caution. Selection bias affecting external validity only—the presence of nondifferential misclassification or selection bias operating on the entire sample,—is manageable as long as one understands the associated limitations. Missing data, and the extent to which non-participation or non-compliance might have affected the results, should always be considered carefully.

---

References

i. Johnson CY. Everyone is biased: Harvard professor’s work reveals we barely know our own minds. Boston Globe. 2013. https://www.boston.com/news/science/...-our-own-minds. Accessed November 27, 2018. (↵ Return)

ii. Bovbjerg M, Siega-Riz A, Evenson K, Goodnight W. Exposure assessment methods affect associations between maternal physical activity and cesarean delivery. J Phys Act Health. 2015;12(1):37-47. (↵ Return 1) (↵ Return 2)

iii. Pregnancy, Infection, and Nutrition (PIN). UNC Gillings School of Global Public Health. https://sph.unc.edu/epid/pregnancy-i...nutrition-pin/. Accessed October 18, 2018.

iv. Evenson KR, Savitz DA, Huston SL. Leisure-time physical activity among pregnant women in the US. Paediatr Perinat Epidemiol. 2004;18(6):400-407. doi:10.1111/j.1365-3016.2004.00595.x (↵ Return)

v. Rothman KJ, Gallacher JEJ, Hatch EE. Why representativeness should be avoided. Int J Epidemiol. 2013;42(4):1012-1014. doi:10.1093/ije/dys223

vi. Beckmann CR, Beckmann CA. Effect of a structured antepartum exercise program on pregnancy and labor outcome in primiparas. J Reprod Med. 1990;35(7):704-709. (↵ Return)

vii. ACOG committee opinion. Exercise during pregnancy and the postpartum period. 2002. American College of Obstetricians and Gynecologists. Int J Gynaecol Obstet Off Organ Int Fed Gynaecol Obstet. 2002;77(1):79-81. (↵ Return)

viii. Physical activity for everyone: Guidelines. Centers for Disease Control and Prevention (CDC). http://www.cdc.gov/physicalactivity/...es/adults.html. Accessed February 10, 2014. (↵ Return)

ix. Dishman RK, Heath GW, Lee I-M. Physical Activity Epidemiology. 2nd ed. Champaign, IL: Human Kinetics; 2013. (↵ Return)

---

1. All research with human participants must be approved by an ethics board, usually called an institutional review board (IRB) in the US. The IRB must approve all study materials, including advertisements, and all such advertisements must clearly state the research question. ↵
2. The astute among you will notice that these recommendations look remarkably like the recommendations^viii for non-pregnant persons. Indeed, barring certain well-defined and relatively rare complications, pregnant women should be just as active as non-pregnant people. ↵
3. Strange but true! ↵