1.7: Confounding

Learning Objectives

After reading this chapter, you will be able to do the following:

1. Explain the concept of confounding, and how it affects the results of epidemiologic studies
2. Reiterate the criteria that a variable must meet to be a possible confounder
3. Conduct a stratified analysis to determine whether a variable is a confounder
4. Provide examples of exposure/outcome/confounder relationships, in terms of confounder criteria and analysis requirements

Like random error and bias, confounding is another threat to study validity. Indeed, there are some texts,^i(p.37) as well as papers,ⁱⁱ that refer to confounding as “confounding bias.” I prefer the term confounding, without the word bias, because while it also leads to a systematic error in the data, confounding is a special case.

Imagine that you are doing a cross-sectional study in elementary school-aged kids of foot size and reading ability:

Figure 7-1

In words, does foot size affect reading ability?

You go to an elementary school and measure both foot size (measured as length in inches) and reading ability (measured in terms of words read per minute, averaged over a 5-minute testing period), and you collect the following data:

Table 7-1

Participant #	Foot Size (inches)	Reading Speed (wpm)
1	7.2	40
2	7.7	85
3	7.2	63
4	7.6	52
5	7.4	51
6	7.1	41
7	7.0	82
8	7.2	60
9	7.6	53
10	7.5	55
11	8.3	123
12	8.2	97
13	8.5	108
14	8.1	111
15	8.2	109
16	8.2	99
17	8.7	95
18	8.0	110
19	8.5	121
20	8.2	108
21	9.4	128
22	8.1	117
23	9.8	115
24	8.8	109
25	9.1	112
26	9.3	112
27	9.8	106
28	9.2	125
29	9.6	163
30	9.0	137

As discussed in chapter 4, in this book we will always dichotomize (i.e., split in two) continuous variables to make the math simpler. If we dichotomize both foot size and reading speed—at 8.25” and 100 wpm, respectively^[1] —we can draw the following 2 x 2 table:

Table 7-2

		Reading Speed
		<100	100+
Foot Size	<8.25″	12	5
	8.25″+	1	12

Because this is a cross-sectional study, we would calculate the odds ratio:

\[\mathrm{OR}=\frac{A D}{B C}=\frac{(12)(12)}{(1)(5)}=28.8\]

In words,

Children with feet that are at least 8.25″ long are 28.8 times as likely to be able to read at least 100 words per minute, compared to children with shorter feet.

Wow! This is a huge finding! Should we give all grade-school kids growth hormones so that they get bigger feet and increase their reading speeds?

Not so fast.

Given that the target population for this hypothetical study is grade-school children, it seems likely that there is a confounder at work—namely, grade level. Kids in higher grades will have bigger feet because they are older, and they will also by and large be faster readers:

Figure 7-2

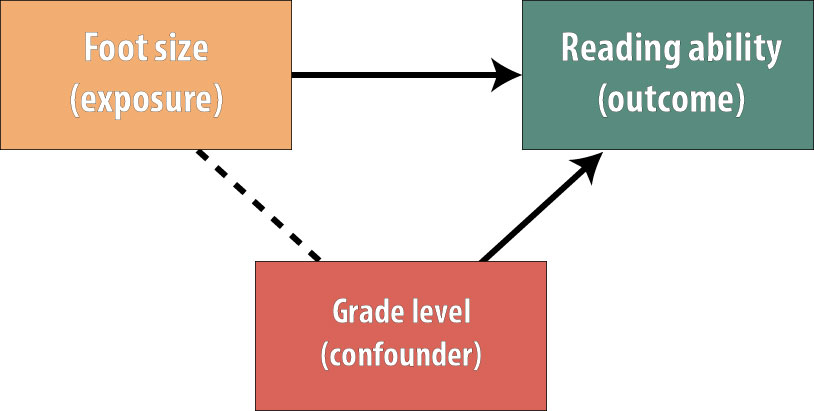
In this scenario, we need to control for the confounder (grade level): we need to remove its influence to get an accurate estimate of the association between the exposure (foot size) and the outcome (reading ability).

Before we delve into how to control for confounders, let’s discuss what confounders are from a theoretical perspective.

Criteria for Confounders

There are 3 criteria that a variable must meet in order for it to be a potential confounder (I say “potential” because not all variables that meet these criteria will actually turn out to confound the data—you figure this out during the analysis):

1. The variable must be statistically associated with the exposure.
2. The variable must cause the outcome.
3. The variable must not be on a causal pathway.

Let’s discuss each of these in more detail.

Criterion #1: Associated with Exposure

Association is a statistical term that does not necessarily imply a causal relationship (this is discussed in more detail later, see chapter 10). Basically, association means that the confounding variable is more common in the exposed group than the unexposed group (or vice versa), thus producing a statistical association. The confounder does not need to cause or prevent the exposure, it just needs to be disproportionately distributed between the exposed and unexposed groups. In our previous example, grade level is disproportionately distributed among various foot sizes—kids in higher grades are more likely to have bigger feet compared to kids in lower grades. Note that there can be a causal relationship, with the confounder causing the exposure (but not the other way around—see criterion 3), but this is not necessary. In our example, grade level is not causing foot size (age is causing foot size)—but they are associated.

Criterion #2: Causes the Outcome

In this case, there must be a causal link between the confounder and the outcome. It does not have to be a proven causal link, just an “it is reasonably possible that this exposure causes (or prevents) that outcome” link. In our foot size/reading ability example, grade level (the confounder) certainly causes faster reading speed (the outcome).

Importantly, the confounder must cause the outcome—not the other way around. If the outcome is causing the confounder, then it’s not a confounder. There are many times in epidemiology when we aren’t sure which way a causal arrow would go—does the disease cause the confounder, or does the confounder cause the disease? An example might be excessive weight loss and illness. Losing a large amount of weight quickly can make one ill—but being ill can also cause a large amount of weight loss. In scenarios like this, where we aren’t sure which way the arrow points, what epidemiologists do in practice is first assume the arrow goes one way and do the analysis accordingly (here, that would mean either including or not the potential confounder). They then assume the arrow goes the other way and do the analysis again. If the results of both analyses are similar, then the arrow direction isn’t important. But if the 2 analyses produce very different results, then we would report both and let the reader decide which is more applicable for them.

Criterion #3: Not on the Causal Pathway

The final criterion for a variable to be a potential confounder is that it is not be on the causal pathway from exposure to outcome. In other words, we do not want this scenario:

Figure 7-3

An example of a variable on a causal pathway might be as follows:

 

Figure 7-4

In this case, “alertness in class” is not a confounder, because it’s caused by the amount of sleep and is thus on the causal pathway. Variables on the causal pathway are mediators, not potential confounders.

Confounding: Definition

A confounder is thus a third variable—not the exposure, and not the outcome^[2]—that biases the measure of association we calculate for the particular exposure/outcome pair.

Importantly, from a research perspective, we never want to report a measure of association that is confounded. Imagine if we do our cross-sectional study on foot size and reading ability, without accounting for grade level. We would report the odds ratio of 28.8 as calculated above…Oops! We’ve reported an association that’s not really true—it’s just confounded by grade level.

Methods of Confounder Control

One can control for confounding through either study design or analytic techniques. In terms of study design, you can

1. Restrict the sample
2. Match on the confounder
3. Randomize (as in, choose a randomized controlled trial as the study design)

Restricting the sample means that you limit your study only to one level of the confounder (e.g., third graders only). Therefore the potentially confounding variable no longer meets the first criterion for confounders—it cannot be disproportionately distributed between exposed and unexposed because there is only one level of the confounder available. Thus all exposed participants are in third grade, as are all unexposed. Our causal diagram now looks like this:

Figure 7-5

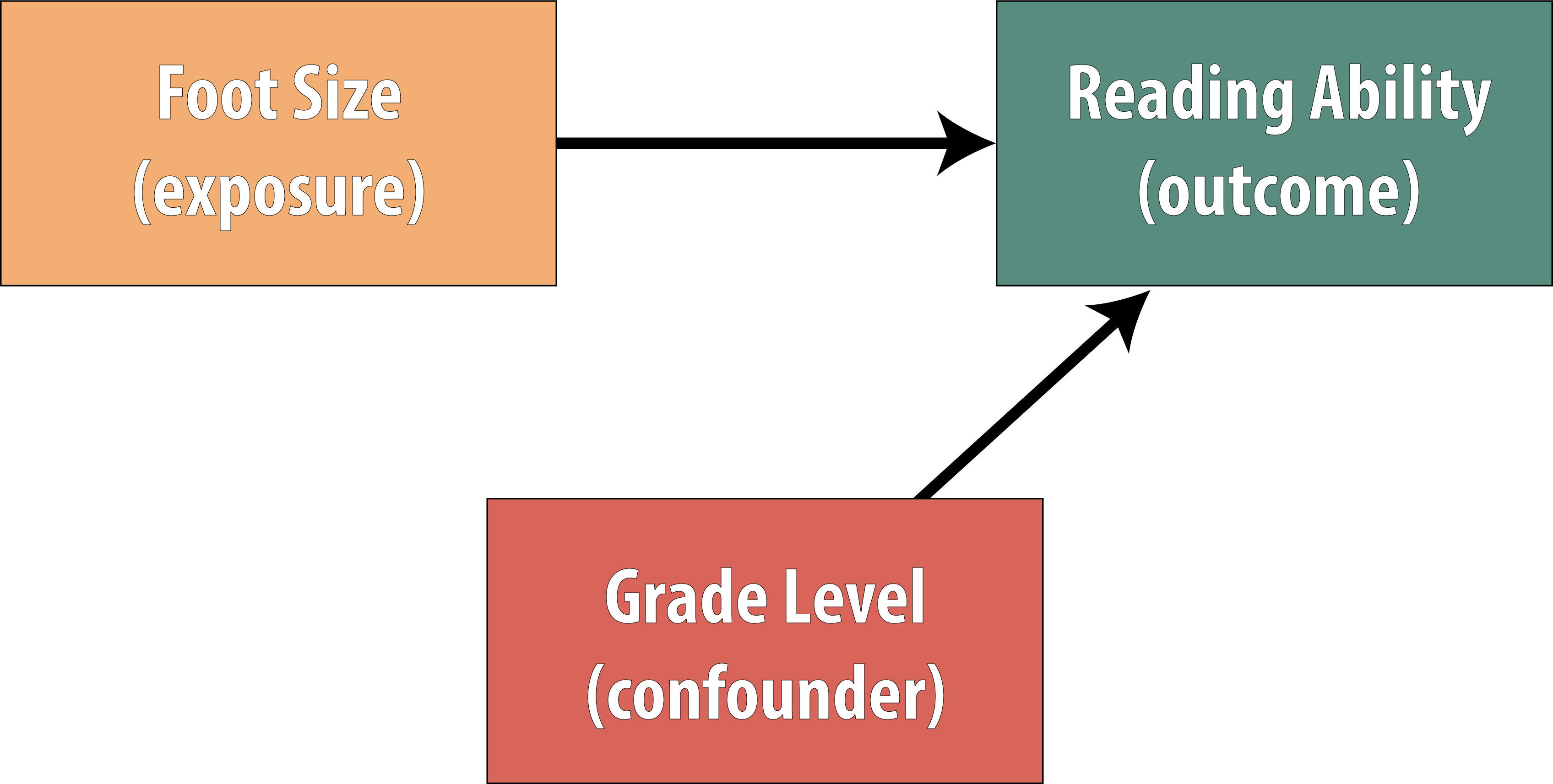
By restricting to just one grade level, we remove the confounding by grade level: kids in both higher and lower grades are no longer relevant because if we have only third graders, then there aren’t any kids in higher or lower grades. Among third-graders only, we would expect that foot size and reading ability are uncorrelated.

Inherent variability

Obviously not all third graders will have the same size feet, nor will all third graders uniformly have the same reading ability. However, on a group level, third graders in general have bigger feet and are better readers than first graders, and likewise have smaller feet and are poorer readers than fifth graders. Epidemiology as a science works because of both this individual variation and the fact that groups of people (selected on some characteristic, like grade level) are more similar to each other than they are to people in other groups.

Here are the same data with a column added for grade level:

Table 7-3

Participant #	Foot Size (inches)	Reading Speed (wpm)	Grade
1	7.2	40	1
2	7.7	85	1
3	7.2	63	1
4	7.6	52	1
5	7.4	51	1
6	7.1	41	1
7	7.0	82	1
8	7.2	60	1
9	7.6	53	1
10	7.5	55	1
11	8.3	123	3
12	8.2	97	3
13	8.5	108	3
14	8.1	111	3
15	8.2	109	3
16	8.2	99	3
17	8.7	95	3
18	8.0	110	3
19	8.5	121	3
20	8.2	108	3
21	9.4	128	5
22	8.1	117	5
23	9.8	115	5
24	8.8	109	5
25	9.1	112	5
26	9.3	112	5
27	9.8	106	5
28	9.2	125	5
29	9.6	163	5
30	9.0	137	5

Limiting ourselves to just third grade, then, the 2 x 2 table looks like this:

Table 7-4

		Reading Speed
		<100	100+
Foot Size	<8.25″	2	2
	8.25″+	3	3

The odds ratio (OR) is 1.0. This is the correct measure of association to report. In reality, foot size has nothing to do with reading speed (OR 1.0). The 28.8 that we calculated earlier was wrong. It was confounded by grade level—there is no association once we control for this confounding by restricting to one grade level.

Though restriction works beautifully in terms of controlling confounding, often it is not a realistic approach because it limits our study too much. For instance, a reasonable study question might be, “What are predictors of breast cancer death among postmenopausal women?” Restricting by age (e.g., “What are predictors of breast cancer death among 62-year-old women?”) would make the study much less useful because we wouldn’t necessarily be able to generalize the results to women of other ages. Epidemiologists thus usually use other approaches for confounder control.

Matching is often used in case-control studies, and it has much the same effect as restriction in controlling confounding. For example, say we are looking at a particular birth defect (outcome) and maternal smoking (exposure), and we suspect that maternal age is a possible confounder. We would want to recruit a control with the same maternal age for each case: if the study were to enroll a 30-year-old case, we would want to match her with a 30-year-old control. The confounder (age) still causes the outcome (birth defects), but by forcing the confounder distribution to be the same between cases and controls, we have negated criterion #2, and thus negated the possible effect of the confounder on the exposure/outcome measure of association.

Randomizing works by forcing the confounder(s) to fail criterion # 1—in this case, by randomly assigning participants to the exposure, we have ensured an equal distribution of the confounder between the exposed and unexposed groups. The link between the confounder and the exposure is now missing, as it is with restriction. See chapter 9 for more on this.

In terms of controlling for confounding in the analysis phase, there are 2 main options:

1. Stratifying
2. Regression (which is really just a special case of stratifying)

To stratify, you take the data and make a different 2 x 2 table for each level of the potential confounder. Let’s now assume that we are concerned with data from a case-control study on oral contraceptive pill (OCP) use (ever used vs. never used) and ovarian cancer:

Figure 7-6

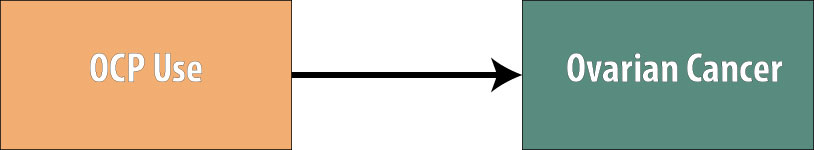
We conduct this study and obtain the following data:

Table 7-5

Participant #	Ever OCP? 0 = no, 1 = yes	Ovarian Cancer? 0 = no (control), 1 = yes (case)
1	1	1
2	1	1
3	1	1
4	1	1
5	0	1
6	0	1
7	0	1
8	0	1
9	0	1
10	0	1
11	1	0
12	1	0
13	1	0
14	1	0
15	0	0
16	0	0
17	0	0
18	0	0
19	0	0
20	0	0

The 2 x 2 table would be as follows:

Table 7-6

		Ovarian Cancer
		+	–
OCP	Ever	4	4
	Never	6	6

The OR is 1.0—use of oral contraceptives is not associated with ovarian cancer. During confounding analyses, this value is referred to as the crude or unadjusted measure of association—meaning that we have not yet accounted, adjusted, or controlled for any confounders. Unadjusted measures only take into account the exposure and the outcome.

However, what about smoking as a confounder? Let’s check the confounder criteria:

1. The variable must be associated with the exposure.
   1. Yes! Both oral contraceptives and smoking increase one’s risk of deep venous thrombosis, a potentially life-threatening condition. Smoking is thus considered a contraindication to oral contraceptive use,ⁱⁱⁱ which leads clinicians to prescribe other forms of birth control instead for women who smoke. This leads to a disproportionate distribution of smokers (the confounder) between women who do and do not use oral contraceptives (the exposure).
2. The variable must cause the outcome.
   1. Possibly. While we often think of smoking as causing lung cancer (which it certainly does), smoking has also been associated with other cancers often enough that it is reasonable to suspect that it might cause ovarian cancer too.^iv
3. The variable must not be on a causal pathway.
   1. Yes! It seems highly unlikely that taking birth control pills would in turn cause a woman to take up smoking.

Smoking thus meets our criteria and is a potential confounder in this scenario.^[3] Here are the data with smoking status added:

Table 7-7

Participant #	Ever OCP? 0 = no, 1 = yes	Ovarian Cancer? 0 = no (control), 1 = yes (case)	Smoker? 0 = no, 1 = yes
1	1	1	1
2	1	1	1
3	1	1	0
4	1	1	0
5	0	1	1
6	0	1	1
7	0	1	1
8	0	1	0
9	0	1	0
10	0	1	0
11	1	1	1
12	1	0	1
13	1	0	0
14	1	0	0
15	0	0	1
16	0	0	1
17	0	0	1
18	0	0	0
19	0	0	0
20	0	0	0

We now stratify by smoking status. In other words, we make 2 different 2 × 2 tables: one for smokers, and the other for nonsmokers. Keep in mind that all the women who appeared in the above 2 × 2 table for ovarian cancer and OCP use are still present—they’re just in one of the two tables below, depending on whether they smoke or not.

Table 7-8: Smokers

		Ovarian Cancer
		+	–
OCP	Ever	2	3
	Never	3	2

Table 7-9: Nonsmokers

		Ovarian Cancer
		+	–
OCP	Ever	2	3
	Never	3	2

Note that the 2 x 2 tables are still for OCP (exposure) and ovarian cancer (outcome)—we have just made one such table for smokers and another for nonsmokers.

The next step in a stratified analysis is to calculate the ORs from these 2 x 2 tables, so we have an OR for smokers, and an OR for nonsmokers.

Confounding Example 1: OCP/Ovarian Cancer by Smoking Status

Example \(\PageIndex{1}\)

The odds ratio for smokers is:

\[\mathrm{OR}_{\text {smokers }}=\frac{A D}{B C}=\frac{(2)(2)}{(3)(3)}=0.44 \nonumber\]

Interpretation:

Women who have ovarian cancer are 0.44 times as likely to report a history of OCP use, compared to women without ovarian cancer—among smokers only.

And the odds ratio for non-smokers is:

\[O R_{\text {non-smokers }}=\frac{A D}{B C}=\frac{(2)(2)}{(3)(3)}=0.44\]

Interpretation:

Among nonsmokers, women who have ovarian cancer are 0.44 times as likely to report a history of oral contraceptive (OCP) use, compared to women without ovarian cancer.

Note the additions (in red) to those interpretations! When conducting stratified analysis, it is important to say which group your measure of association applies to. This can come either at the beginning (as it does above for nonsmokers) or at the end (as it does above for smokers).

Since our stratum-specific odds ratios (0.44 for smokers and 0.44 for nonsmokers) are similar to each other but different from the crude OR (which was 1.0), we say that smoking is indeed acting as a confounder in these data. The crude OR was wrong; it was confounded by smoking.

“Similar” and “Different”—by How Much?

When the stratum-specific measures of association are similar to each other but different than the crude OR, we have confounding. But by how much? There is a standard criterion for “different”—if the crude and adjusted ORs are more than 10% different, most epidemiologists would consider that to be evidence of confounding. For “similar,” though, there isn’t really a consensus. Perhaps within 2–3% of each other? Importantly, the crude value does not fall between them.

When the stratum-specific measures of association are similar to each other but different than the crude OR, we have confounding. But by how much? There is a standard criterion for “different”—if the crude and adjusted ORs are more than 10% different, most epidemiologists would consider that to be evidence of confounding. For “similar,” though, there isn’t really a consensus. Perhaps within 2–3% of each other? Importantly, the crude value does not fall between them.

The “real” OR is 0.44: oral contraceptive use is rather strongly associated with less ovarian cancer. But without accounting for smoking, it looks like this is not true (the crude OR was 1.0, and did not control for smoking). Because there is confounding, we thus would want to report an OR that controls for smoking (the confounder). The most common way to do this is to calculate an “adjusted” measure. There are many ways to calculate an adjusted measure of association^[4]; one is to calculate the Mantel-Haenzel odds ratio:

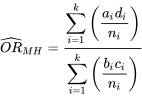
\[\widehat{O R_{M H}}=\frac{\sum_{i=1}^{k}\left(\frac{a_{i} d_{i}}{n_{i}}\right)}{\sum_{i=1}^{k}\left(\frac{b_{i} c_{i}}{n_{i}}\right)}\]

where \(n_{i}=a_{i}+b_{i}+c_{i}+d_{i}\)

You can see from the formula that the Mantel-Haenzel OR is just a weighted average of the stratum-specific odds ratios, with each stratum being an i. We call this the adjusted OR, and it has controlled for confounding by the variable on which we stratified.

Categorizing Continuous Variables

I mentioned in chapter 4 that if one has a continuous variable (e.g., age or height), most analyses are best served by keeping that variable continuous but that for the purposes of this book, we would dichotomize all variables to make the math easier. If a potential confounder is a continuous variable, we must categorize it (into 2 or 3 categories, usually) in order to conduct a stratified analysis by hand. Thus if height were our potential confounder, we might create 3 categories: less than 5′2″, 5′2″–6′0″, and taller than 6′0″. You can see, however, that within these categories, there is still considerable variability—5′2″ is a full 10″ shorter than 6′. Thus creating categories (i.e., strata for the stratified analysis) out of a continuous variable in order to control confounding might not work perfectly if the strata remain too heterogeneous. This produces residual confounding—we have removed some of the confounding by height but there is still some confounding left. This is one reason epidemiologists mostly jump straight to regression, in which it is easier to keep continuous variables continuous. However, the goal of this book is to create knowledgeable readers of epidemiologic studies, not knowledgeable doers, which would substantially more training. I thus rely on categorizing continuous variables so that the math is easy to follow and statistical software is unnecessary. If you follow the math as presented here, it is easy enough to make the cognitive leap to reading papers that use regression (regression is just stratified analysis with many more categories).

Most studies reported in the literature use the other method for controlling for confounding in analyses: regression, which is just a special case of a stratified analysis—specifically, it accounts for all possible strata. For instance, if we had continuous data on total months of smoking over the course of a lifetime, a regression model would “make” a 2 × 2 table for nonsmokers, then one for people had smoked for 1 month, then a 2 × 2 table for those who had smoked for 2 months, and so on, until each possible stratum had its own 2 × 2 table. The model then calculates a weighted average of the total of these (much like a mega–Mantel Haenzel), and the result is also known as the adjusted odds ratio. For cohort studies or randomized controlled trials we of course instead calculate the adjusted risk ratio or adjusted rate ratio (RR).

Interpretation

To interpret our OCP/ovarian cancer findings in words (the adjusted odds ratio, whether calculated via Mantel-Haenzel or by regression, is 0.44), we would say:

Women who have ovarian cancer are 0.44 times as likely to report a history of OCP use compared to women without ovarian cancer, controlling for smoking.

Or we could say:

Women who have ovarian cancer are 0.44 times as likely to report a history of OCP use compared to women without ovarian cancer, adjusting for smoking.

Or we could say:

Women who have ovarian cancer are 0.44 times as likely to report a history of oral contraceptive use compared to women without ovarian cancer, holding smoking constant.

Notice how there are multiple ways of letting the reader know that smoking was treated as a confounder (phrases in red). It doesn’t matter which you choose—the important thing is that you make it clear that we are presenting the measure of association having already dealt with the confounding.

Choosing Confounders

When conducting an analysis in real life, there are often multiple potential confounders. The first step in any analysis is to make a list of all such potential confounders. The easiest way to do this is first to make a list of all variables that might cause your outcome. Then take that list and make sure the variables are associated with the exposure. Finally, for any confounders that meet our first 2 criteria, make sure they are not on the causal pathway (e.g., that the exposure is not causing the confounder). As mentioned above, there are many instances where it is difficult to know which is causing which; in such cases, we do the analysis both ways.

The next step would be to determine which of the potential confounders meeting the 3 criteria to control for in an analysis (regression allows you to control for many confounders at once). One way would be to drop all confounders that do not meet the “10% change” criterion mentioned above. There are additional nuances, however, that are beyond the scope of this book, and prominent epidemiologists differ in their opinions on how to choose a list of confounders to control for.^v,vi,vii Luckily, beginning epidemiology students will not need to conduct their own complex analyses; however, being able to think through a particular exposure/disease relationship and make a list of all potential confounders is a useful skill when reading the literature. Did the authors consider all the variables you thought of that meet the confounder criteria? If not, did they explicitly specify why not? If an obvious potential confounder is missing from the analysis in a particular article, then maybe that is not the most valid article.

Summary

Confounders are variables—not the exposure and not the outcome—that affect the data in undesirable and unpredictable ways. Specifically, in data that are confounded, one will calculate the wrong measure of association (and it is impossible to know in which direction one is wrong). This leads to inaccurate conclusions unless one controls for that confounder. To be a potential confounder, the variable must be statistically associated with the exposure, must cause the outcome, and must not be on the causal pathway. Potential confounders can be controlled for via study design (restriction, matching, or randomization) or during data analysis (stratification or regression, leading to an adjusted measure of association). In the latter case, if the crude and adjusted estimates of association are more than 10% different, the variable should be considered a confounder, and one would report the adjusted estimate because it controls for the confounder.

---

References

i. Last JM. A Dictionary of Epidemiology. 4th ed. 2001. New York: Oxford University Press. (↵ Return)

ii. Goldstein BA, Bhavsar NA, Phelan M, Pencina MJ. Controlling for informed presence bias due to the number of health encounters in an electronic health record. Am J Epidemiol. 2016;184(11):847-855. doi:10.1093/aje/kww112 (↵ Return)

iii. Bonnema RA, McNamara MC, Spencer AL. Contraception choices in women with underlying medical conditions. Am Fam Physician. 2010;82(6):621-628. (↵ Return)

iv. Study: Smoking causes almost half of deaths from 12 cancer types. American Cancer Society. https://www.cancer.org/latest-news/s...cer-types.html. Accessed October 21, 2018. (↵ Return)

v. Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiologic research. Epidemiol Camb Mass. 1999;10(1):37-48. (↵ Return)

vi. Harrell FEJ. Regression Modeling Strategies, with Applications to Linear Models, Logistic Regression, and Survival Analysis. New York: Springer; 2001. (↵ Return)

vii. Selvin S. Statistical Analysis of Epidemiologic Data. 3rd ed. Oxford: Oxford University Press; 2004. (↵ Return)

---

1. The 8.25” and 100 wpm cutoffs would be a great thing to vary in a sensitivity analysis! See chapter 6. ↵
2. Just a reminder! When epidemiologists say outcome we mean “health outcome or disease under study”—we do not mean the results of a study. Those are results. See Appendix 1. ↵
3. Remember, variables that meet the confounder criteria are potential confounders. They may or may not actually produce a biased estimate of association; we figure this out during the analysis. ↵
4. Any biostatistics text would discuss several such methods. ↵