7.3: Heat
- Page ID
- 15255
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To relate heat transfer to temperature change.
- Memorize temperature equations for Celsius, Fahrenheit and Kelvin conversions.
- Understand how body temperature can vary.
The concept of temperature may seem familiar to you, but many people confuse temperature with heat. Temperature is a measure of how hot or cold an object is relative to another object (its thermal energy content), whereas heat is the flow of thermal energy between objects with different temperatures. When we touch a hot object, energy flows from the hot object into our fingers, and we perceive that incoming energy as the object being “hot.” Conversely, when we hold an ice cube in our palms, energy flows from our hand into the ice cube, and we perceive that loss of energy as “cold.” In both cases, the temperature of the object is different from the temperature of our hand, so we can conclude that differences in temperatures are the ultimate cause of heat transfer.
Temperature Scales
Temperature is a measure of the average amount of energy of motion, or kinetic energy, a system contains. Temperatures are expressed using scales that use units called degrees. There are three scales used for reporting temperatures. Figure \(\PageIndex{1}\) compares the three temperature scales: Fahrenheit (expressed as °F), Celsius (°C), and Kelvin (K). Thermometers measure temperature by using materials that expand or contract when heated or cooled. Mercury or alcohol thermometers, for example, have a reservoir of liquid that expands when heated and contracts when cooled, so the liquid column lengthens or shortens as the temperature of the liquid changes.
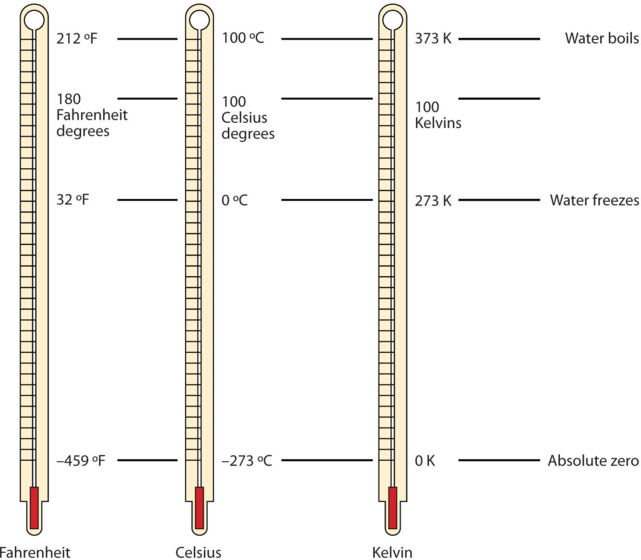 Figure \(\PageIndex{1}\): Fahrenheit, Celsius, and Kelvin Temperatures. A comparison of the three temperature scales. These thermometers have a red-colored liquid which contains alcohol and food coloring. Silver looking thermometers contain mercury, which is a neurotoxin.
Figure \(\PageIndex{1}\): Fahrenheit, Celsius, and Kelvin Temperatures. A comparison of the three temperature scales. These thermometers have a red-colored liquid which contains alcohol and food coloring. Silver looking thermometers contain mercury, which is a neurotoxin.
In the United States, the commonly used temperature scale is the Fahrenheit scale (symbolized by °F and spoken as “degrees Fahrenheit”). On this scale, the freezing point of liquid water (the temperature at which liquid water turns to solid ice) is 32 °F, and the boiling point of water (the temperature at which liquid water turns to steam) is 212 °F.
Science also uses other scales to express temperature. For example, the Celsius scale (symbolized by °C and spoken as “degrees Celsius”) defines 0°C as the freezing point of water and 100 °C as the boiling point of water. This scale is divided into 100 divisions between these two landmarks and extended higher and lower as well. By comparing the Fahrenheit and Celsius scales, a conversion between the two scales can be determined:
\[^{\circ}C= \left(^{\circ}F-32\right )\times \dfrac{5}{9} \label{F2C} \]
\[^{\circ}F= \left(^{\circ}C\times \dfrac{9}{5}\right)+32 \label{C2F} \]
Note that science uses the Celsius and Kelvin scales almost exclusively; virtually no practicing chemist expresses laboratory-measured temperatures with the Fahrenheit scale. (In fact, the United States is one of the few countries in the world that still uses the Fahrenheit scale on a daily basis. People driving near the borders of Canada or Mexico may pick up local radio stations on the other side of the border that express the daily weather in degrees Celsius, so do not get confused by their weather reports.)
- What is 98.6°F in degrees Celsius?
- What is 25.0°C in degrees Fahrenheit?
Solution
- Using Equation \ref{F2C}, we have
\[\begin{align*} ^{\circ}C &= (98.6-32)\times \dfrac{5}{9} \\[5pt] &=66.6\times \dfrac{5}{9} \\[5pt] &= 37.0^{\circ}C \end{align*} \nonumber \]
- Using Equation \ref{C2F}, we have
\[\begin{align*} ^{\circ}F &= (25.0\times \dfrac{9}{5})+32 \\[5pt] &= 45.0+32 \\[5pt] &=77.0^{\circ}F \end{align*} \nonumber \]
For more examples of how to perform these types of problems, click on this video to see your professor in action.
- Convert 0°F to degrees Celsius.
- Convert 212°C to degrees Fahrenheit.
- Answer a
-
−17.8°C
- Answer b
-
414°F
The fundamental unit of temperature in SI is the Kelvin (K). The Kelvin temperature scale (note that the name of the scale capitalizes the word Kelvin, but the unit itself is lowercase) uses degrees that are the same size as the Celsius degree, but the numerical scale is shifted up by 273.15 units. That is, the conversion between the Kelvin and Celsius scales is as follows:
\[K=^{\circ}C+273.15 \label{C2K} \]
For most purposes, it is acceptable to use 273 instead of 273.15 in Equation \ref{C2K}.
Note that the Kelvin scale does not use the word degrees; a temperature of 295 K is spoken of as “two hundred ninety-five kelvin” and not “two hundred ninety-five degrees Kelvin.”
The reason that the Kelvin scale is defined this way is that there exists a minimum possible temperature called absolute zero (zero Kelvin). The Kelvin temperature scale is set so that 0 K is absolute zero, and the temperature is counted upward from there. Normal room temperature is about 295 K, as seen in the following example.
If the normal room temperature is 72.0°F, what is room temperature in degrees Celsius and kelvin?
Solution
First, we use Equation \ref{F2C} to determine the temperature in degrees Celsius:
\[\begin{align*} ^{\circ}C &= (72.0-32)\times \dfrac{5}{9} \\[5pt] &= 40.0\times \dfrac{5}{9} \\[5pt] &= 22.2^{\circ}C \end{align*} \nonumber \]
Then we use Equation \ref{C2K} to determine the temperature in the Kelvin scale:
\[\begin{align*} K &= 22.2^{\circ}C+273.15 \\[5pt] &= 295.4K \end{align*} \nonumber \]
So, room temperature is about 295 K.
Normal body temperature is defined as being 98.6°F (+/- 1.0°F). To determine body temperature, thermometers can be placed inside or on the surface of the body. The two best methods of obtaining body temperature are placing the thermometer either under the tongue or inside the rectum. Typically, children are capable of holding a thermometer in their mouths around the age of four (have fun before that age).
Fever is defined as body temperature being above 100°F (adults). High fever status occurs at and above 104°F. For adults, these adults should seek medical attention immediately if the fever exceeds 104°F. For children, these values are much lower.
Hyperthermia (inability of the body to regulate heat) occurs when normal body temperature is exceeded. Conditions that can cause hyperthermia are fever (infection), heat stroke, thyroid disorders, heart attack, or traumatic injury. Medications for cancer, arthritis, and thyroid patients can cause the body temperature to rise. Symptoms of hyperthermia include sweating, confusion, nausea, and dizziness.
Hypothermia (exposure to cold environments) occurs when normal body temperature dips below 95.0°F. When this occurs, the affected person(s) should seek immediate medical attention. During hypothermia, the body has problems producing heat. Medical conditions like diabetes, infection, and thyroid dysfunction can cause hypothermia. Watch this video of American Marines attempting to survive extreme environments. Symptoms of this condition involve shivering, confusion, and sluggish behavior.
Treating hyperthermia could involve hydrating a patient. If a fever is due to infection, analgesics (like Tylenol, Advil, aspirin, or Aleve) can help alleviate fever. Placing someone in a cool bath can also relieve symptoms.
To combat hypothermia, one must remove wet clothing, redress in warm materials, and participate in physical movement.
Heat transfer
Heat is a familiar manifestation of energy. When we touch a hot object, energy flows from the hot object into our fingers, and we perceive that incoming energy as the object being “hot.” Conversely, when we hold an ice cube in our palms, energy flows from our hand into the ice cube, and we perceive that loss of energy as “cold.” In both cases, the temperature of the object is different from the temperature of our hand, so we can conclude that differences in temperatures are the ultimate cause of heat transfer.
Suppose we consider the transfer of heat from the opposite perspective—namely, what happens to a system that gains or loses heat? Generally, the system’s temperature changes. (We will address a few exceptions later.) The greater the original temperature difference, the greater the transfer of heat, and the greater the ultimate temperature change. The relationship between the amount of heat transferred and the temperature change can be written as
\[\text{heat} \propto ΔT \label{Eq1} \]
where ∝ means “is proportional to” and ΔT is the change in temperature of the system. Any change in a variable is always defined as “the final value minus the initial value” of the variable, so ΔT is Tfinal − Tinitial. In addition, the greater the mass of an object, the more heat is needed to change its temperature. We can include a variable representing mass (m) to the proportionality as follows:
\[\text{heat} \propto mΔT \label{Eq2} \]
To change this proportionality into an equality, we include a proportionality constant. The proportionality constant is called the specific heat and is commonly symbolized by \(c\):
\[\text{heat} = mcΔT \label{Eq3} \]
Every substance has a characteristic specific heat, which is reported in units of cal/g•°C or cal/g•K, depending on the units used to express ΔT. The specific heat of a substance is the amount of energy that must be transferred to or from 1 g of that substance to change its temperature by 1°. Table \(\PageIndex{1}\) lists the specific heats for various materials.
| Substance | c (cal/g•°C) |
|---|---|
| aluminum (Al) | 0.215 |
| aluminum oxide (Al2O3) | 0.305 |
| benzene (C6H6) | 0.251 |
| copper (Cu) | 0.092 |
| ethanol (C2H6O) | 0.578 |
| hexane (C6H14) | 0.394 |
| hydrogen (H2) | 3.419 |
| ice [H2O(s)] | 0.492 |
| iron (Fe) | 0.108 |
| iron(III) oxide (Fe2O3) | 0.156 |
| mercury (Hg) | 0.033 |
| oxygen (O2) | 0.219 |
| sodium chloride (NaCl) | 0.207 |
| steam [H2O(g)] | 0.488 |
| water [H2O(ℓ)] | 1.00 |
The proportionality constant c is sometimes referred to as the specific heat capacity or (incorrectly) the heat capacity.
The direction of heat flow is not shown in heat = mcΔT. If energy goes into an object, the total energy of the object increases, and the values of heat ΔT are positive. If energy is coming out of an object, the total energy of the object decreases, and the values of heat and ΔT are negative.
What quantity of heat is transferred when a 150.0 g block of iron metal is heated from 25.0°C to 73.3°C? What is the direction of heat flow?
Solution
We can use Equation \ref{Eq3} to determine the amount of heat, but first we need to determine ΔT. Because the final temperature of the iron is 73.3°C and the initial temperature is 25.0°C, ΔT is as follows:
\[\begin{align*} ΔT = T_{final} − T_{initial} \\[4pt] &= 73.3^oC − 25.0^oC \\[4pt] &= 48.3^oC \end{align*} \nonumber \]
The mass is given as 150.0 g, and Table \(\PageIndex{1}\) gives the specific heat of iron as 0.108 cal/g•°C. Substitute the known values into Equation \ref{Eq3} and solve for amount of heat:
\[\mathrm{heat=(150.0\: g)\left(0.108\: \dfrac{cal} {g\cdot {^\circ C}}\right)(48.3^\circ C) = 782\: cal} \nonumber \]
Note how the gram and °C units cancel algebraically, leaving only the calorie unit, which is a unit of heat. Because the temperature of the iron increases, energy (as heat) must be flowing into the metal.
Exercise \(\PageIndex{3}\)
What quantity of heat is transferred when a 295.5 g block of aluminum metal is cooled from 128.0°C to 22.5°C? What is the direction of heat flow?
- Answer
-
6,700 cal
A 10.3 g sample of a reddish-brown metal gave off 71.7 cal of heat as its temperature decreased from 97.5°C to 22.0°C. What is the specific heat of the metal? Can you identify the metal from the data in Table \(\PageIndex{1}\)?
Solution
The question gives us the heat, the final and initial temperatures, and the mass of the sample. The value of ΔT is as follows:
ΔT = Tfinal − Tinitial = 22.0°C − 97.5°C = −75.5°C
If the sample gives off 71.7 cal, it loses energy (as heat), so the value of heat is written as a negative number, −71.7 cal. Substitute the known values into heat = mcΔT and solve for c:
−71.7 cal = (10.3 g)(c)(−75.5°C)
\(c \,\mathrm{=\dfrac{-71.7\: cal}{(10.3\: g)(-75.5^\circ C)}}\)
c = 0.0923 cal/g•°C
This value for specific heat is very close to that given for copper in Table \(\PageIndex{1}\).
Exercise \(\PageIndex{4}\)
A 10.7 g crystal of sodium chloride (NaCl) had an initial temperature of 37.0°C. What is the final temperature of the crystal if 147 cal of heat were supplied to it?
- Answer
-
103.4°C
Notice that water has a very high specific heat compared to most other substances. Water is commonly used as a coolant for machinery because it is able to absorb large quantities of heat (see table above). Coastal climates are much more moderate than inland climates because of the presence of the ocean. Water in lakes or oceans absorbs heat from the air on hot days and releases it back into the air on cool days.
 Figure \(\PageIndex{2}\): This power plant in West Virginia, like many others, is located next to a large lake so that the water from the lake can be used as a coolant. Cool water from the lake is pumped into the plant, while warmer water is pumped out of the plant and back into the lake.
Figure \(\PageIndex{2}\): This power plant in West Virginia, like many others, is located next to a large lake so that the water from the lake can be used as a coolant. Cool water from the lake is pumped into the plant, while warmer water is pumped out of the plant and back into the lake.
Summary
- Heat transfer is related to temperature change.
- Thespecific heat of a substance is the amount of energy required to raise the temperature of 1 gram of the substance by \(1^\text{o} \text{C}\).

