7.4: Phase Changes
- Page ID
- 15256
- Determine the heat associated with a phase change.
Matter can exist in one of several different states, including a gas, liquid, or solid state. The amount of energy in molecules of matter determines the state of matter.
- A gas is a state of matter in which atoms or molecules have enough energy to move freely. The molecules come into contact with one another only when they randomly collide.
- A liquid is a state of matter in which atoms or molecules are constantly in contact but have enough energy to keep changing positions relative to one another.
- A solid is a state of matter in which atoms or molecules do not have enough energy to move. They are constantly in contact and in fixed positions relative to one another.
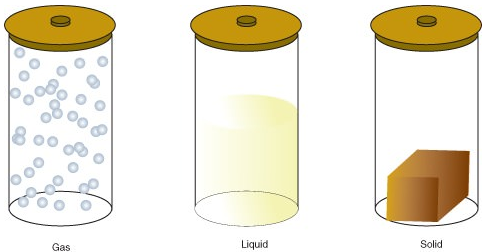 Figure \(\PageIndex{1}\): States of Matter. All three containers contain a substance with the same mass, but the substances are in different states. In the left-hand container, the substance is a gas, which has spread to fill its container. It takes both the shape and volume of the container. In the middle container, the substance is a liquid, which has spread to take the shape of its container but not the volume. In the right-hand container, the substance is a solid, which takes neither the shape nor the volume of its container.
Figure \(\PageIndex{1}\): States of Matter. All three containers contain a substance with the same mass, but the substances are in different states. In the left-hand container, the substance is a gas, which has spread to fill its container. It takes both the shape and volume of the container. In the middle container, the substance is a liquid, which has spread to take the shape of its container but not the volume. In the right-hand container, the substance is a solid, which takes neither the shape nor the volume of its container.
The following are the changes of state:
| Solid → Liquid | Melting or fusion |
|---|---|
| Liquid → Gas | Vaporization |
| Liquid → Solid | Freezing |
| Gas → Liquid | Condensation |
| Solid → Gas | Sublimation |
- If heat is added to a substance, such as in melting, vaporization, and sublimation, the process is endothermic. In this instance, heat is increasing the speed of the molecules causing them move faster (examples: solid to liquid; liquid to gas; solid to gas).
- If heat is removed from a substance, such as in freezing and condensation, then the process is exothermic. In this instance, heat is decreasing the speed of the molecules causing them move slower (examples: liquid to solid; gas to liquid). These changes release heat to the surroundings.
- The amount of heat needed to change a sample from solid to liquid would be the same to reverse from liquid to solid. The only difference is the direction of heat transfer.
Label each of the following processes as endothermic or exothermic.
- water boiling
- ice forming on a pond
Solution
- endothermic - you must put a pan of water on the stove and give it heat in order to get water to boil. Because you are adding heat/energy, the reaction is endothermic.
- exothermic - think of ice forming in your freezer instead. You put water into the freezer, which takes heat out of the water, to get it to freeze. Because heat is being pulled out of the water, it is exothermic. Heat is leaving.
Exercise \(\PageIndex{1}\)
Label each of the following processes as endothermic or exothermic.
- water vapor condensing
- gold melting
- Answer
-
a. exothermic
b. endothermic
A phase change is a physical process in which a substance goes from one phase to another. Usually the change occurs when adding or removing heat at a particular temperature, known as the melting point or the boiling point of the substance. The melting point is the temperature at which the substance goes from a solid to a liquid (or from a liquid to a solid). The boiling point is the temperature at which a substance goes from a liquid to a gas (or from a gas to a liquid). The nature of the phase change depends on the direction of the heat transfer. Heat going into a substance changes it from a solid to a liquid or a liquid to a gas. Removing heat from a substance changes a gas to a liquid or a liquid to a solid.
Two key points are worth emphasizing. First, at a substance’s melting point or boiling point, two phases can exist simultaneously. Take water (H2O) as an example. On the Celsius scale, H2O has a melting point of 0°C and a boiling point of 100°C. At 0°C, both the solid and liquid phases of H2O can coexist. However, if heat is added, some of the solid H2O will melt and turn into liquid H2O. If heat is removed, the opposite happens: some of the liquid H2O turns into solid H2O. A similar process can occur at 100°C: adding heat increases the amount of gaseous H2O, while removing heat increases the amount of liquid H2O (Figure \(\PageIndex{1}\)).
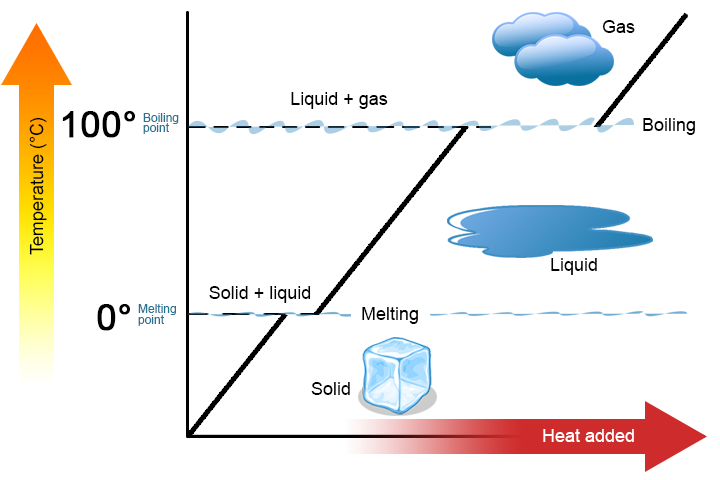 Figure \(\PageIndex{2}\): Heating curve for water. As heat is added to solid water, the temperature increases until it reaches 0 °C, the melting point. At this point, the phase change, added heat goes into changing the state from a solid to liquid. Only when this phase change is complete, the temperature can increase. (CC BY 3.0 Unported; Community College Consortium for Bioscience Credentials).
Figure \(\PageIndex{2}\): Heating curve for water. As heat is added to solid water, the temperature increases until it reaches 0 °C, the melting point. At this point, the phase change, added heat goes into changing the state from a solid to liquid. Only when this phase change is complete, the temperature can increase. (CC BY 3.0 Unported; Community College Consortium for Bioscience Credentials).
Water is a good substance to use as an example because many people are already familiar with it. Other substances have melting points and boiling points as well.
Second, as shown in Figure \(\PageIndex{1}\), the temperature of a substance does not change as the substance goes from one phase to another. In other words, phase changes are isothermal (isothermal means “constant temperature”). Again, consider H2O as an example. Solid water (ice) can exist at 0°C. If heat is added to ice at 0°C, some of the solid changes phase to make liquid, which is also at 0°C. Remember, the solid and liquid phases of H2O can coexist at 0°C. Only after all of the solid has melted into liquid does the addition of heat change the temperature of the substance.
For each phase change of a substance, there is a characteristic quantity of heat needed to perform the phase change per gram (or per mole) of material. The heat of fusion (ΔHfus) is the amount of heat per gram (or per mole) required for a phase change that occurs at the melting point. The heat of vaporization (ΔHvap) is the amount of heat per gram (or per mole) required for a phase change that occurs at the boiling point. If you know the total number of grams or moles of material, you can use the ΔHfus or the ΔHvap to determine the total heat being transferred for melting or solidification using these expressions:
\[\text{heat} = n \times ΔH_{fus} \label{Eq1a} \]
where \(n\) is the number of moles and \(ΔH_{fus}\) is expressed in energy/mole or
\[\text{heat} = m \times ΔH_{fus} \label{Eq1b} \]
where \(m\) is the mass in grams and \(ΔH_{fus}\) is expressed in energy/gram.
For the boiling or condensation, use these expressions:
\[\text{heat} = n \times ΔH_{vap} \label{Eq2a} \]
where \(n\) is the number of moles) and \(ΔH_{vap}\) is expressed in energy/mole or
\[\text{heat} = m \times ΔH_{vap} \label{Eq2b} \]
where \(m\) is the mass in grams and \(ΔH_{vap}\) is expressed in energy/gram.
Remember that a phase change depends on the direction of the heat transfer. If heat transfers in, solids become liquids, and liquids become solids at the melting and boiling points, respectively. If heat transfers out, liquids solidify, and gases condense into liquids. At these points, there are no changes in temperature as reflected in the above equations.
How much heat is necessary to melt 55.8 g of ice (solid H2O) at 0°C? The heat of fusion of H2O is 79.9 cal/g.
Solution
We can use the relationship between heat and the heat of fusion (Equation \(\PageIndex{1}\)) to determine how many cal of heat are needed to melt this ice:
\[ \begin{align*} \ce{heat} &= \ce{m \times ΔH_{fus}} \\[4pt] \mathrm{heat} &= \mathrm{(55.8\: \cancel{g})\left(\dfrac{79.9\: cal}{\cancel{g}}\right)=4,460\: cal} \end{align*} \nonumber \]
How much heat is necessary to vaporize 685 g of H2O at 100°C? The heat of vaporization of H2O is 540 cal/g.
- Answer
-
\[ \begin{align*} \ce{heat} &= \ce{m \times ΔH_{vap}} \\[4pt] \mathrm{heat} &= \mathrm{(685\: \cancel{g})\left(\dfrac{540\: cal}{\cancel{g}}\right)=370,000\: cal} \end{align*} \nonumber \]
Table \(\PageIndex{1}\) lists the heats of fusion and vaporization for some common substances. Note the units on these quantities; when you use these values in problem solving, make sure that the other variables in your calculation are expressed in units consistent with the units in the specific heats or the heats of fusion and vaporization.
| Substance | ΔHfus (cal/g) | ΔHvap (cal/g) |
|---|---|---|
| aluminum (Al) | 94.0 | 2,602 |
| gold (Au) | 15.3 | 409 |
| iron (Fe) | 63.2 | 1,504 |
| water (H2O) | 79.9 | 540 |
| sodium chloride (NaCl) | 123.5 | 691 |
| ethanol (C2H5OH) | 45.2 | 200.3 |
| benzene (C6H6) | 30.4 | 94.1 |
There is also a phase change where a solid goes directly to a gas:
\[\text{solid} \rightarrow \text{gas} \label{Eq3} \]
This phase change is called sublimation. Each substance has a characteristic heat of sublimation associated with this process. For example, the heat of sublimation (ΔHsub) of H2O is 620 cal/g.
We encounter sublimation in several ways. You may already be familiar with dry ice, which is simply solid carbon dioxide (CO2). At −78.5°C (−109°F), solid carbon dioxide sublimes, changing directly from the solid phase to the gas phase:
\[\mathrm{CO_2(s) \xrightarrow{-78.5^\circ C} CO_2(g)} \label{Eq4} \]
Solid carbon dioxide is called dry ice because it does not pass through the liquid phase. Instead, it does directly to the gas phase. (Carbon dioxide can exist as liquid but only under high pressure.) Dry ice has many practical uses, including the long-term preservation of medical samples.
Even at temperatures below 0°C, solid H2O will slowly sublime. For example, a thin layer of snow or frost on the ground may slowly disappear as the solid H2O sublimes, even though the outside temperature may be below the freezing point of water. Similarly, ice cubes in a freezer may get smaller over time. Although frozen, the solid water slowly sublimes, redepositing on the colder cooling elements of the freezer, which necessitates periodic defrosting (frost-free freezers minimize this redeposition). Lowering the temperature in a freezer will reduce the need to defrost as often.
Under similar circumstances, water will also sublime from frozen foods (e.g., meats or vegetables), giving them an unattractive, mottled appearance called freezer burn. It is not really a “burn,” and the food has not necessarily gone bad, although it looks unappetizing. Freezer burn can be minimized by lowering a freezer’s temperature and by wrapping foods tightly so water does not have any space to sublime into.
Key Takeaway
- There is an energy change associated with any phase change.

