7.5: Bond Energies
- Page ID
- 15257
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Learning Objectives of this Module are to:
- Define bond energy.
- Calculate enthalpy change or heat of reaction.
- Determine if a chemical process is exothermic or endothermic.
What happens when you take a basketball, place it halfway up a playground slide, and then let it go? The basketball rolls down the slide. What happens if you do it again? Does the basketball roll down the slide? It should.
If you were to perform this experiment over and over again, do you think the basketball would ever roll up the slide? Probably not. Why not? Well, for starters, in all of our experience, the basketball has always moved to a lower position when given the opportunity. The gravitational attraction of Earth exerts a force on the basketball, and given the chance, the basketball will move down. We say that the basketball is going to a lower gravitational potential energy. The basketball can move up the slide, but only if someone exerts some effort (that is, work) on the basketball. A general statement, based on countless observations over centuries of study, is that all objects tend to move spontaneously to a position of minimum energy unless acted on by some other force or object.
Bond Energy
A similar statement can be made about atoms in compounds. Atoms bond together to form compounds because in doing so they attain lower energies than they possess as individual atoms. A quantity of energy, equal to the difference between the energies of the bonded atoms and the energies of the separated atoms, is released, usually as heat. That is, the bonded atoms have a lower energy than the individual atoms do. When atoms combine to make a compound, energy is always given off, and the compound has a lower overall energy. In making compounds, atoms act like a basketball on a playground slide; they move in the direction of decreasing energy.
We can reverse the process, just as with the basketball. If we put energy into a molecule, we can cause its bonds to break, separating a molecule into individual atoms. Bonds between certain specific elements usually have a characteristic energy, called the bond energy, that is needed to break the bond. The same amount of energy was liberated when the atoms made the chemical bond in the first place. The term bond energy is usually used to describe the strength of interactions between atoms that make covalent bonds. A C–C bond has an approximate bond energy of 80 kcal/mol, while a C=C has a bond energy of about 145 kcal/mol. The C=C bond is stronger than C-C (as discussed in relation to bond length in Section 4.4). For atoms in ionic compounds attracted by opposite charges, the term lattice energy is used. For now, we will deal with covalent bonds in molecules.
Although each molecule has its own characteristic bond energy, some generalizations are possible. For example, although the exact value of a C–H bond energy depends on the particular molecule, all C–H bonds have a bond energy of roughly the same value because they are all C–H bonds. It takes roughly 100 kcal of energy to break 1 mol of C–H bonds, so we speak of the bond energy of a C–H bond as being about 100 kcal/mol. Table \(\PageIndex{1}\) lists the approximate bond energies of various covalent bonds.
| Bond | Bond Energy (kcal/mol) |
|---|---|
| C–H | 100 |
| C–O | 86 |
| C=O | 190 |
| C–N | 70 |
| C–C | 85 |
| C=C | 145 |
| C≡C | 200 |
| N–H | 93 |
| H–H | 105 |
| Br-Br | 46 |
| Cl–Cl | 58 |
| O–H | 110 |
| O=O | 119 |
| H–Br | 87 |
| H–Cl | 103 |
When a chemical reaction occurs, the atoms in the reactants rearrange their chemical bonds to make products. The new arrangement of bonds does not have the same total energy as the bonds in the reactants. Therefore, when chemical reactions occur, there will always be an accompanying energy change. The enthalpy change, for a given reaction can be calculated using the bond energy values from Table \(\PageIndex{1}\).
Enthalpy Change or Heat of Reaction, ΔH
Energy changes in chemical reactions are usually measured as changes in enthalpy. In this process, one adds energy to the reaction to break bonds, and extracts energy for the bonds that are formed.
\[\text{enthalpy change} ≈ \sum (\text{bonds broken}) - \sum (\text{bonds formed}) \nonumber \]
The ≈ sign is used because we are adding together average bond energies (i.e., over many different molecules). Hence, this approach does not give exact values for the enthalpy change, ΔH.
Let’s consider the reaction of 2 mols of hydrogen gas (H2) with 1 mol of oxygen gas (O2) to give 2 mol water:
\[\ce{2H_2(g) + O_2(g) \rightarrow 2H_2O(g)} \nonumber \]
or shown graphically:
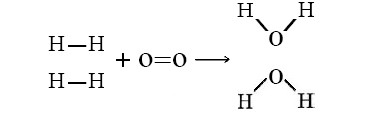
with these average bond energies involved:
- \(\ce{H–H}\) = 105 kcal/mol
- \(\ce{O=O}\) = 119 kcal/mol
- \(\ce{O–H}\) = 110 kcal/mol
In this reaction, 2 H–H bonds and 1 O=O bonds are broken, while 4 O–H bonds (two for each H2O) are formed. The energy changes can be tabulated and calculated as follows:
| Bonds Broken (kcal/mol) | Bonds Formed (kcal/mol) | ||
|---|---|---|---|
| 2 H–H | 2 mol x 105 kcal/mol = 210 kcal | 4 O–H | 4 mols x 110 kcal/mol = 440 kcal |
| 1 O=O | 1 mol x 119 kcal/mol = 119 kcal | ||
| Total = 329 kcal | Total = 440 kcal | ||
\[\begin{align*} \Delta H &≈ \sum (\text{bonds broken}) - \sum (\text{bonds formed}) \\[4pt] &≈ 329 \: \text{kcal} - 440 \: \text{kcal} \\[4pt] &≈ −111 \: \text{kcal} \end{align*} \nonumber \]
The enthalpy change (ΔH) of the reaction is approximately −111 kcal/mol. This means that bonds in the products (440 kcal) are stronger than the bonds in the reactants (329 kcal) by about 111 kcal/mol. Because the bonds in the products are stronger than those in the reactants, the reaction releases more energy than it consumes. This excess energy is released as heat, so the reaction is exothermic. Hence, we can re-write the reaction with the heat released (111 kcal) on the product side of the equation, as follows:
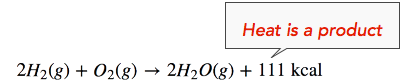
We can also re-write the reaction equation with the ΔH information (see below). Note that an exothermic reaction has a negative ΔH value.
\[\ce{2H_2(g)+O_2(g) \rightarrow 2H_2O(g)} \ \: \: \: \: \: \Delta H = -111 \: \text{kcal} \nonumber \]
What is the enthalpy change for this reaction? Is the reaction exothermic or endothermic?
\[\ce{H_2(g) + Br_2(g) \rightarrow 2HBr(g)} \nonumber \]
Solution
Step 1- First look at the equation and identify which bonds exist on in the reactants (bonds broken).
- one H-H bond and
- one Br-Br bond
Step 2- Do the same for the products (bonds formed)
- two H-Br bonds
Step 3- Identify the bond energies of these bonds from Table \(\PageIndex{1}\):
- H-H bonds: 105 kcal/mol
- Br-Br bonds: 46 kcal/mol
Step 4- Set up the table (see below) and apply the formula for enthalpy change.
| Bonds Broken (kcal/mol) | Bonds Formed (kcal/mol) | ||
|---|---|---|---|
| 1 H–H | 1 mol x 105 kcal/mol = 105 kcal | 2 H–Br | 2 mols x 87 kcal/mol = 174 kcal |
| 1 Br–Br | 1 mol x 46 kcal/mol = 46 kcal | ||
| Total = 151 kcal | Total = 174 kcal | ||
\[\begin{align*} \Delta H &≈ 151 \: \text{kcal} - 174 \: \text{kcal} \\[4pt] &≈ −23 \: \text{kcal} \end{align*} \nonumber \]
Step 5- Since \(ΔH\) is negative (−23 kcal), the reaction is exothermic.
Exercise \(\PageIndex{1}\)
Using the bond energies given in the chart above, find the enthalpy change for the thermal decomposition of water:
\[\ce{H_2(g) + Cl_2(g) \rightarrow 2HCl(g)} \nonumber \]
Is the reaction written above exothermic or endothermic? Explain.
- Answer
-
ΔH = −43 kcal
Since ΔH is negative (−43 kcal), the reaction is exothermic.
Endothermic and Exothermic Reactions
Endothermic and exothermic reactions can be thought of as having energy as either a reactant of the reaction or a product. Endothermic reactions require energy, so energy is a reactant. Heat flows from the surroundings to the system (reaction mixture) and the enthalpy of the system increases (ΔH is positive). As discussed in the previous section, in an exothermic reaction, heat is released (considered a product) and the enthalpy of the system decreases (ΔH is negative).
In the course of an endothermic process, the system gains heat from the surroundings and so the temperature of the surroundings decreases (gets cold). A chemical reaction is exothermic if heat is released by the system into the surroundings. Because the surroundings is gaining heat from the system, the temperature of the surroundings increases. See Figure \(\PageIndex{1}\).
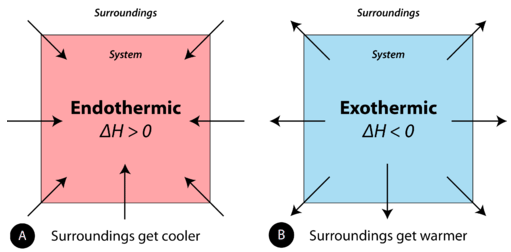 Figure \(\PageIndex{1}\): (A) Endothermic reaction. (B) Exothermic reaction.
Endothermic reaction: surroundings get cooler and delta H is greater than 0, Exothermic reaction: surroundings get warmer and delta H is less than 0
Figure \(\PageIndex{1}\): (A) Endothermic reaction. (B) Exothermic reaction.
Endothermic reaction: surroundings get cooler and delta H is greater than 0, Exothermic reaction: surroundings get warmer and delta H is less than 0
Endothermic Reaction: When \(1 \: \text{mol}\) of calcium carbonate decomposes into \(1 \: \text{mol}\) of calcium oxide and \(1 \: \text{mol}\) of carbon dioxide, \(177.8 \: \text{kJ}\) of heat is absorbed. Because the heat is absorbed by the system, the \(177.8 \: \text{kJ}\) is written as a reactant. The ΔH is positive for an endothermic reaction.

\[\ce{CaCO_3} \left( s \right) \rightarrow \ce{CaO} \left( s \right) + \ce{CO_2} \left( g \right) \: \: \: \: \: \Delta H = +177.8 \: \text{kJ} \nonumber \]
Exothermic Reaction: When methane gas is combusted, heat is released, making the reaction exothermic. Specifically, the combustion of \(1 \: \text{mol}\) of methane releases 890.4 kilojoules of heat energy. This information can be shown as part of the balanced equation in two ways. First, the amount of heat released can be written in the product side of the reaction. Another way is to write the heat of reaction (ΔH) information with a negative sign, \(-890.4 \: \text{kJ}\).
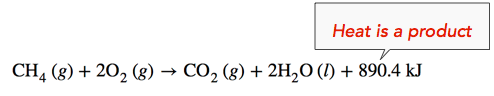
\[\ce{CH_4} \left( g \right) + 2 \ce{O_2} \left( g \right) \rightarrow \ce{CO_2} \left( g \right) + 2 \ce{H_2O} \left( l \right) \: \: \: \: \: \Delta H = -890.4 \: \text{kJ} \nonumber \]
Is each chemical reaction exothermic or endothermic?
- CH4(g) + 2O2(g) → CO2(g) + 2H2O(ℓ) + 213 kcal
- N2(g) + O2(g) + 45 kcal → 2NO(g)
Solution
- Because energy (213 kcal) is a product, energy is given off by the reaction. Therefore, this reaction is exothermic.
- Because energy (45 kcal) is a reactant, energy is absorbed by the reaction. Therefore, this reaction is endothermic.
Is each chemical reaction exothermic or endothermic?
- H2(g) + F2(g) → 2HF (g) + 130 kcal
- 2C(s) + H2(g) + 5.3 kcal → C2H2(g)
- Answer
-
a. The energy (130 kcal) is produced, hence the reaction is exothermic
b. The energy (5.3 kcal) is supplied or absorbed to react, hence, the reaction is endothermic
Energy Diagrams
Endothermic and exothermic reactions can be visually represented by energy-level diagrams like the ones in Figure \(\PageIndex{2}\). In endothermic reactions, the reactants have higher bond energy (stronger bonds) than the products. Strong bonds have lower potential energy than weak bonds. Hence, the energy of the reactants is lower than that of the products. This type of reaction is represented by an "uphill" energy-level diagram shown in Figure \(\PageIndex{2A}\). For an endothermic chemical reaction to proceed, the reactants must absorb energy from their environment to be converted to products.
In an exothermic reaction, the bonds in the product have higher bond energy (stronger bonds) than the reactants. In other words, the energy of the products is lower than the energy of the reactants, hence is energetically downhill, shown in Figure \(\PageIndex{2B}\). Energy is given off as reactants are converted to products. The energy given off is usually in the form of heat (although a few reactions give off energy as light). In the course of an exothermic reaction, heat flows from the system to its surroundings, and thus, gets warm.
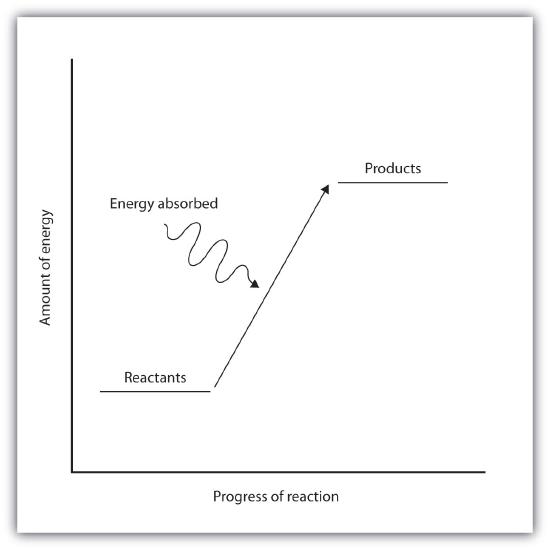 Figure \(\PageIndex{2A}\): Endothermic Reactions
Figure \(\PageIndex{2A}\): Endothermic Reactions
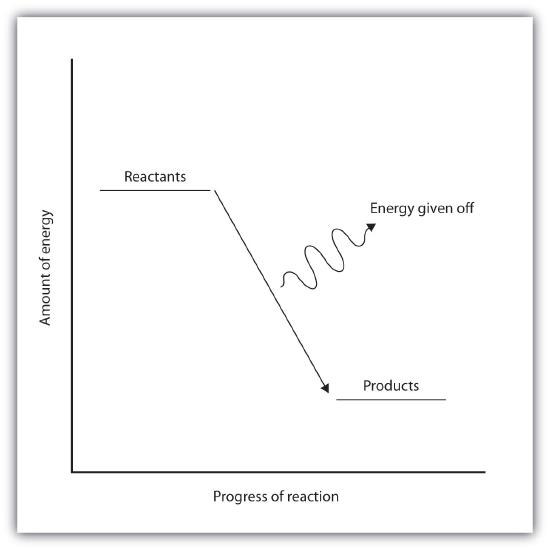 Figure \(\PageIndex{2B}\): Exothermic Reactions
Figure \(\PageIndex{2B}\): Exothermic Reactions
| Endothermic Reactions | Exothermic Reactions |
|---|---|
| Heat is absorbed by reactants to form products. | Heat is released. |
| Heat is absorbed from the surroundings; as a result, the surroundings get cold. | Heat is released by the reaction to surroundings; surroundings feel hot. |
| ΔHrxn is positive | ΔHrxn is negative |
| The bonds broken in the reactants are stronger than the bonds formed in the products | The bonds formed in the products are stronger than the bonds broken in the reactants |
| The reactants are lower in energy than the products | The products are lower in energy than the reactants |
| Represented by an "uphill" energy diagram | Represented by an "downhill" energy diagram |
Key Takeaways
- Atoms are held together by a certain amount of energy called bond energy.
- Energy is required to break bonds. Energy is released when chemical bonds are formed because atoms become more stable.
- Chemical processes are labeled as exothermic or endothermic based on whether they give off or absorb energy, respectively.

