8.4: pH and Kw
- Page ID
- 59984
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Skills to Develop
- To define the pH scale as a measure of acidity of a solution
Because of its amphoteric nature (i.e., acts as both an acid or a base), water does not always remain as \(H_2O\) molecules. In fact, two water molecules react to form hydronium and hydroxide ions:
\[ 2\, H_2O \;(l) \rightleftharpoons H_3O^+ \;(aq) + OH^− \; (aq) \label{Eq1}\]
This is also called the self-ionization of water. The concentration of \(H_3O^+\) and \(OH^-\) are equal in pure water because of the 1:1 stoichiometric ratio of Equation \(\ref{Eq1}\). The molarity of H3O+ and OH- in water are also both \(1.0 \times 10^{-7} \,M\) at 25° C. Therefore, a constant of water (\(K_w\)) is created to show the equilibrium condition for the self-ionization of water. The product of the molarity of hydronium and hydroxide ion is always \(1.0 \times 10^{-14}\).
\[K_w= [H_3O^+][OH^-] = 1.0 \times 10^{-14} \label{2}\]
This equations also applies to all aqueous solutions. However, \(K_w\) does change at different temperatures, which affects the pH range discussed below.
Note
\(H^+\) and \(H_3O^+\) is often used interchangeably to represent the hydrated proton, commonly call the hydronium ion.
pH
Because Kw is constant (\(1.0 \times 10^{-14}\) at 25 °C, the pKw is 14, the constant of water determines the range of the pH scale. To understand what the pKw is, it is important to understand first what the "p" means in pOH, and pH. The Danish biochemist Søren Sørenson proposed the term pH to refer to the "potential of hydrogen ion." He defined the "p" as the negative of the logarithm, -log, of [H+]. Therefore the pH is the negative logarithm of the molarity of H. The pOH is the negative logarithm of the molarity of OH- and the pKwis the negative logarithm of the constant of water. These definitions give the following equations:
\[pH= -\log [H^+] \label{4a}\]
\[pOH= -\log [OH^-] \label{4b}\]
\[pK_w= -\log [K_w] \label{4c}\]
A logarithm, used in the above equations, of a number is how much a power is raised to a particular base in order to produce that number. To simplify this, look at the equation: logba=x. This correlates to bx=a. A simple example of this would be \(\log_{10}100=2\), or \(10^2=100\). It is assumed that the base of Logarithms is ten if it is not stated. So for the sake of pH and pOH problems it will always be ten. When x is a negative number that means you are dividing it by the power. So, if \(log_{10} 0.01=-2\) which can be written \(10^{-2}=0.01\), then \(10^-2\) also means \(1/10^2\). The log function can be found on your scientific calculator. Now if we apply this to pH and pOH we can better understand how we calculate the values.
At room temperature,
\[K_w =1.0 \times 10^{-14} \label{4d}\]
So
\[pK_w=-\log [1.0 \times 10^{-14}] \label{4e}\]
Using the properties of logarithms, Equation \(\ref{4e}\) can be rewritten as
\[10^{-pK_w}=10^{-14}. \label{4f}\]
By substituting, we see that pKw is 14. The equation also shows that each increasing unit on the scale decreases by the factor of ten on the concentration of \(H^+\). For example, a pH of 1 has a molarity ten times more concentrated than a solution of pH 2.
Since
\[pK_w\ = 14 \label{5a}\]
\[pK_w= pH + pOH = 14 \label{5b}\]
Note
The pH scale is logarithmic, meaning that an increase or decrease of an integer value changes the concentration by a tenfold. For example, a pH of 3 is ten times more acidic than a pH of 4. Likewise, a pH of 3 is one hundred times more acidic than a pH of 5. Similarly a pH of 11 is ten times more basic than a pH of 10.
The Effective Range of the pH Scale
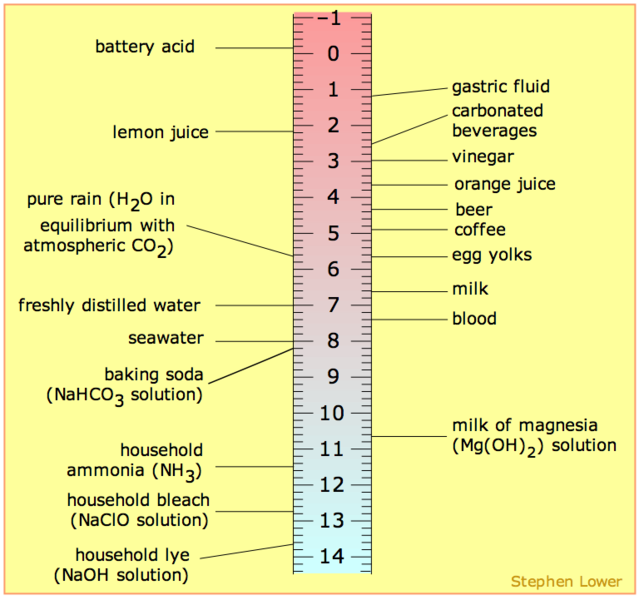
It is common that the pH scale is argued to range from 0-14 or perhaps 1-14 but neither is correct. The pH range does not have an upper nor lower bound, since as defined above, the pH is an indication of concentration of H+. For example, at a pH of zero the hydronium ion concentration is one molar, while at pH 14 the hydroxide ion concentration is one molar. Typically the concentrations of H+ in water in most solutions fall between a range of 1 M (pH=0) and 10-14 M (pH=14). Hence a range of 0 to 14 provides sensible (but not absolute) "bookends" for the scale (Figure \(\PageIndex{1}\)). One can go somewhat below zero and somewhat above 14 in water, because the concentrations of hydronium ions or hydroxide ions can exceed one molar. Figure 1 depicts the pH scale with common solutions and where they are on the scale.
Figure \(\PageIndex{1}\): Solutions and the placement of them on pH scale
- From the range 7-14, a solution is basic. The pOH should be looked in the perspective of OH- instead lf H+. Whenever the value of pOH is greater than 7, then it is considered basic. And therefore there are more OH- than H+ in the solution
- At pH 7, the substance or solution is at neutral and means that the concentration of H+ and OH- ion is the same.
- From the range 1-7, a solution is acidic. So, whenever the value of a pH is less than 7, it is considered acidic. There are more H+ than OH- in an acidic solution.
Note
The pH scale does not have an upper nor lower bound. Negative pH values are possible
The following PhET simulation helps to build an intuition of the pH scale.
Example \(\PageIndex{1}\)
If the concentration of \(NaOH\) in a solution is \(2.5 \times 10^{-4}\; M\), what is the concentration of \(H_3O^+\)?
SOLUTION
Because
\[1.0 \times 10^{-14} = [H_3O^+][OH^-] \nonumber\]
to find the concentration of H3O+, solve for the [H3O+].
\[\dfrac{1.0 \times 10^{-14}}{[OH^-]} = [H_3O^+] \nonumber\]
\[\dfrac{1.0 \times 10^{-14}}{2.5 \times 10^{-4}} = [H_3O^+] = 4.0 \times 10^{-11}\; M \nonumber\]
Example \(\PageIndex{2}\)
- Find the pH of a solution of 0.002 M of HCl.
- Find the pH of a solution of 0.00005 M NaOH.
SOLUTION
- The equation for pH is -log [H+]
\[[H^+]= 2.0 \times 10^{-3}\; M \nonumber\]
\[pH = -\log [2.0 \times 10^{-3}] = 2.70 \nonumber \]
- The equation for pOH is -log [OH-]
\[ [OH^-]= 5.0 \times 10^{-5}\; M \nonumber\]
\[pOH = -\log [5.0 \times 10^{-5}] = 4.30 \nonumber\]
\[pK_w = pH + pOH \nonumber\]
and
\[pH = pK_w - pOH \nonumber\]
then
\[pH = 14 - 4.30 = 9.70 \nonumber\]
Living Systems
Molecules that make up or are produced by living organisms usually function within a narrow pH range (near neutral) and a narrow temperature range (body temperature). Many biological solutions, such as blood, have a pH near neutral. pH influences the structure and the function of many enzymes (protein catalysts) in living systems. Many of these enzymes have narrow ranges of pH activity (Table \(\PageIndex{1}\)).
| Compartment | pH |
| Gastric Acid | 1 |
| Lysosomes | 4.5 |
| Granules of Chromaffin Cells | 5.5 |
| Human Skin | 5.5 |
| Urine | 6 |
| Neutral H2O at 37 °C | 6.81 |
| Cytosol | 7.2 |
| Cerebrospinal Fluid | 7.3 |
| Blood | 7.43-7.45 |
| Mitochondrial Matrix | 7.5 |
| Pancreas Secretions | 8.1 |
Cellular pH is so important that death may occur within hours if a person becomes acidotic (having increased acidity in the blood). As one can see pH is critical to life, biochemistry, and important chemical reactions. Common examples of how pH plays a very important role in our daily lives are given below:
- Water in swimming pool is maintained by checking its pH. Acidic or basic chemicals can be added if the water becomes too acidic or too basic.
- Whenever we get a heartburn, more acid build up in the stomach and causes pain. We needs to take antacid tablets (a base) to neutralize excess acid in the stomach.
- The pH of blood is slightly basic. A fluctuation in the pH of the blood can cause in serious harm to vital organs in the body.
- Certain diseases are diagnosed only by checking the pH of blood and urine.
- Certain crops thrive better at certain pH range.
- Enzymes activate at a certain pH in our body.
Contributors
- Emmellin Tung (UCD), Sharon Tsao (UCD), Divya Singh (UCD), Patrick Gormley (Lapeer Community School District)