1.3: Pharmacokinetics I
- Page ID
- 10624
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describe the physicochemical and physiological factors that influence the absorption of drugs from enteral and parenteral routes of administration, their distribution within the body, and their routes and mechanisms of elimination.
- Explain how dose, bioavailability, rate of absorption, apparent volume of distribution, total clearance, and elimination half-life affect the plasma concentrations of a drug after administration of a single dose.
- Describe the factors which determine the time-course of systemic accumulation of a drug administered by infusion or multiple doses.
Absorption of Drugs
- Transport Across Cell Membranes
- Passive diffusion
- Passage through lipid cell membrane by dissolution in membrane; rate dependent on concentration gradient and lipid:water partition coefficient of drug; rate markedly higher for unionized form of weak electrolyte because of its higher lipophilicity than the ionized form; obeys first-order kinetics (rate of transport is proportional to concentration gradient at transport site).
- Filtration through aqueous channels within membranes and between cells.
- Active transport
- Passage facilitated by an energy-dependent membrane carrier mechanism such that transport can occur against a concentration gradient; transporters include the family of ATP-dependent proteins, such as
- the multidrug resistance p-glycoprotein (amphipathic cationic and neutral substrates, 170 kD, mdr gene product, verapamil sensitive)
- the multidrug resistance-associated proteins (MRP1-6, organic anion substrates, 190 kD, probenecid sensitive).
- Exhibits structural selectivity, saturability, competition between structural analogues and genetic variants.
- Sites for drugs in intestinal mucosa (cell to lumen), capillary endothelium of brain and testis (cell to blood), choroid plexus (CSF to blood), proximal renal tubular cell (blood to urine), hepatocyte (blood to bile), tumor cells (efflux pump).
- Obeys Michaelis-Menten kinetics: if drug concentration is high enough to saturate carrier mechanism, kinetics are zero-order (rate of transport is constant).
- Passage facilitated by an energy-dependent membrane carrier mechanism such that transport can occur against a concentration gradient; transporters include the family of ATP-dependent proteins, such as
- Endocytosis
- Passage into cell within membrane invagination.
- Important mechanism for particulates and high molecule weight compounds, such as proteins.
- Passive diffusion
- Routes of Drug Administration
- General determinants of absorption rate
- Dissolution into aqueous fluids at absorption site, lipid solubility, concentration gradient, blood flow at absorption site, surface area of absorption site.
- Importance of rate-limiting process
- Oral (p.o.) Ingestion
- Convenient route for administration of solid as well as liquid formulations.
- Additional variables which may influence rate and extent of absorption include disintegration and dissolution of solids, acidity of gastric contents, gastric emptying rate, intraluminal and mucosal biotransformation by host or bacterial enzymes, dietary contents, and presence of other drugs.
- First-pass effect: absorbed drug passes via portal circulation through liver which may clear substantial fraction and thus decrease bioavailability (percent of dose which reaches the systemic circulation).
- Parenteral Injection
- Subcutaneous (s.c.) and intramuscular (i.m.) administration: more extensive absorption of high molecular weight, polar molecules than by oral route, via lymphatic circulation; absorption rate can be manipulated by formulation, e.g. rapid from aqueous solution, slow from suspension or solid pellet.
- Intravenous (i.v.) injection: complete bioavailability; drugs only given in sterile solution; important when immediate effect required; increased risk of toxicity.
- Pulmonary Inhalation
- Rapid absorption of drugs in gaseous, vaporized or aerosol form.
- Absorption of particulates/aerosols depends on particle/droplet size which influences depth of entry in pulmonary tree; 1-5 uM particles reach alveolus
- Topical Application
- Usually for local effect; patch formulations for systemic effect
- Absorption through mucous membrane may be rapid.
- Absorption through skin generally slow; enhanced by increased lipophilicity, by damage to stratum corneum, and by increased blood flow.
- General determinants of absorption rate
- Distribution of Drugs
- Tissue differences in rates of uptake of drugs.
- Blood flow: distribution occurs most rapidly into tissues with high blood flow (lungs, kidneys, liver, brain) and least rapidly in tissues with low flow (fat).
- Capillary permeability: permeability of capillaries is tissue dependent;distribution rates relatively slower into CNS because of tight junction between capillary endothelial cells, insignificant aqueous membrane pores, juxtaposed glial cells around endothelium and efflux transporters in vascular endothelium ("blood-brain barrier"); capillaries of liver and kidney more porous.
- Differences in tissue/blood ratios at equilibrium
- Dissolution of lipid-soluble drugs in adipose tissue
- Binding of drugs to intracellular sites
- Plasma protein binding; many drugs reversibly bind to albumin, α1-acidglycoprotein or other proteins in plasma; extent of binding dependent on affinity, number of binding sites, and drug concentrations; drug bound to albumin is not filtered by renal glomerulus but may be cleared by proximal renal tubule and liver; binding reduces free drug available for distribution into tissue; many drug interactions based on displacement from binding sites.
- Apparent Volume of Distribution (Vd)
- Fluid compartments of 70-kg subject in liters and as percent of body weight: plasma 3 l (4%), extracellular water 12 l (17%), total body water 41 l (58%).
- Estimation of Vd from extrapolated plasma concentration at "zero-time" (Co) after intravenous administration:
\[\mathbf{V}_d={Dose \over \mathbf{C}_o}\]
- Prediction of Vd from chemical characteristics of drug, e.g. high lipid solubility, high Vd
- The plasma half-life of a drug (the time to reduce the concentration by one- half) is directly proportional to Vd, and inversely proportional to total clearance (ClT); for a given ClT, the higher the Vd, the longer the t1/2:
\[\mathbf{t}_{1 \over 2}={ln2(\mathbf{V}_d )\over \mathbf{Cl}_T}\]
- Tissue differences in rates of uptake of drugs.
Elimination of Drugs
- Total Clearance (ClT)
- Volume of plasma completely cleared of drug per unit time by all routes and mechanisms.
- Summation of clearance values for each route, generally:
\[\mathbf{CL}_T={\mathbf {Cl}_{renal} + \mathbf{Cl}_{hepatic}}\]
- If intrinsic capacity of an organ to clear drug is high and exceeds plasma flow to that organ, then the clearance equals plasma flow and is altered by changes in plasma flow.
- The plasma half-life of a drug is inversely proportional to total clearance, and directly proportional to Vd; for a given Vd, the higher the total clearance, the shorter the half-life.
- Biotransformation
- Elimination of drug by chemical modification of the molecule by spontaneous or (more usually) enzymatically catalyzed reaction. Drug may be biotransformed by reactions at several sites on the molecule.
- Product(s) may have greater, lesser or qualitatively different pharmacologic activity from parent compound. A prodrug is inactive and is biotransformed to a therapeutic agent. Highly reactive products such as quinones or epoxides may cause tissue necrosis or DNA damage.
- Reaction rate dependent on chemical structure and obeys Michaelis-Menten kinetics (usually first-order at therapeutic drug concentrations).
- Enzymatic activity generally highest in liver; enzymes in target organ may be responsible for conversion of drug to therapeutic or toxic metabolite; enzymes in intestinal bacteria may facilitate enterohepatic circulation of drug conjugates excreted in bile.
- Sources of individual variation in rates of biotransformation: chemical exposures (drugs, dietary constituents and supplements, smoke); genetics; age; disease
- Major pathways of hepatic biotransformation
- Phase I: often first step in biotransformation with formation of product susceptible to phase II conjugative reaction
- Phase II: Coupling of drug or its oxidized metabolite to endogenous conjugating agent derived form carbohydrate, protein or sulfur sources; generally products more water-soluble and more readily excreted in urine or bile.
- Excretion
- Elimination of drug by excretion unchanged in body fluid or breath.
- Routes of excretion
- Urine: quantitatively most important excretory route for nonvolatile drugs and their metabolites; excretion rate depends on rate of glomerular filtration (drug not bound to plasma proteins), proximal tubular active secretion, and passive reabsorption
1) Determination of renal clearance (ClR), the volume of plasma completely cleared of drug per unit time (ml/min).
\[ {Cl}_R={{excreation\ rate\ i urine}\over plasma\ concentration }\]
Measure the amount of drug excreted in the urine during a time interval t1 to t2. Find the plasma concentration of the drug at the midpoint of the time interval, (t1+ t2)/2, by interpolating on the ln Cp vs. t plot.
\[ {Cl}_R=[{ amount\ excreted \ from\ {t}_1\ to\ {t}_2\over ( {t}_2- {t}_1)}]\over {C}_p\ at {{( {t}_1 + {t}_2)}\over2}\]
2) Mechanism of renal excretion can be inferred by comparison of ClR to that of an indicator of glomerular filtration (creatinine), i.e., greater than 120 ml/min in 70-kg subject indicates tubular secretion and less than that indicates net reabsorption (if no plasma binding); maximum renal clearance = renal plasma flow (e.g. para-aminohippuric acid, 650 ml/min in 70-kg subject).
3) Factors modifying ClR: extent of plasma protein binding (displacement enhances glomerular filtration), urinary pH (reabsorption of drugs with ionizable group is dependent on urinary pH; raising the pH promotes excretion of acids, impairs excretion of bases), renal disease (creatinine clearance or its estimate from serum creatinine provides a useful clinical indicator of impaired renal function and is approximately proportional to drug renal clearance; the effect of renal impairment on the total clearance of a drug can be estimated from the ClCR and the nonrenal clearance).
- Bile: quantitatively important excretory route for drugs and their metabolites which are actively transported by hepatocyte; once in small intestine, compounds with sufficient lipophilicity are reabsorbed and cleared again by liver (enterohepatic circulation), more polar substances may be biotransformed by bacteria (e.g. hydrolysis of drug conjugates) and products reabsorbed; unabsorbed drugs and metabolites are excreted in feces.
- Minor routes: sweat, tears, reproductive fluids, milk; generally pH- dependent passive diffusion of lipophilic drugs; can be of toxicologic significance e.g. exposure of infants to drugs in milk.
- Urine: quantitatively most important excretory route for nonvolatile drugs and their metabolites; excretion rate depends on rate of glomerular filtration (drug not bound to plasma proteins), proximal tubular active secretion, and passive reabsorption
Time Course of Plasma Concentrations
- Relationship between plasma concentration and drug effect: minimum effective concentration, latency, duration of effect, time and magnitude of peak effect
- Time-course of plasma concentrations for a single dose
- Case with Highly Rapid Absorption Relative to Elimination
- Single compartment model
1) First -order elimination: drug assumed to rapidly equilibrate into volume of distribution; plasma concentrations decline according to first-order kinetics; elimination rate from plasma is proportional to plasma concentration, fraction eliminated per unit time is elimination rate constant (kel).
\[{ {dC}_p\over dt}=- {k}_{el} {C}_p\]
\[ {C}_p= {C}_0e^{- {k}_{el}t}\]
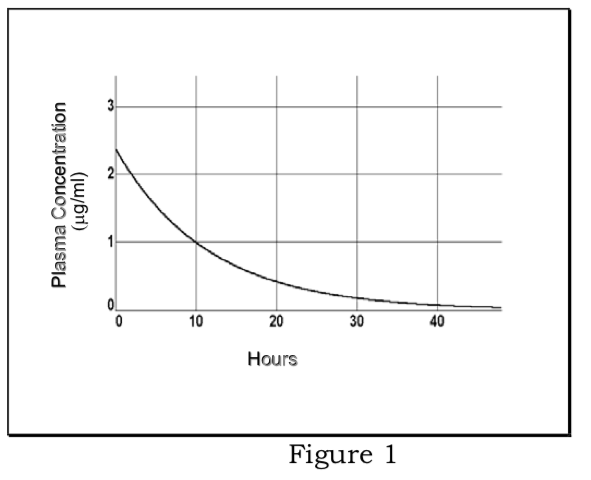
Determination of elimination rate constant and elimination half-life:
\[ {lnC}_p=ln {C}_0- {k}_{el}t\]
Plot of ln Cp vs. t is a straight line with slope of -kel. Plasma half-life (t1/2 =.693/kel) is constant and independent of dose.
Determination of apparent volume of distribution:
Extrapolation to time zero of the line of best fit for ln Cp vs t data; antilog of drug concentration at time 0 designated as C0. Then,
\[ {V}_d (in\ mls\ or\ liters)={Total\ Dose\over {C}_0}\]
Determination of total clearance:
According to definitions above, total clearance is the mass of drug (Cp Vd) eliminated per unit time divided by the plasma concentration; therefore,
\[ {Cl}_T={( {k}_{el})( {C}_p\cdot {V}_d)\over {C}_p}={( {k}_{el})( {V}_d)}=[{0.693\over {t}_{1/2}}]( {V}_d)\]
Determination of nonrenal clearance (ClNR):
If total clearance and renal clearance are determined from plasma and urine samples as described above, then clearance by nonrenal routes (which includes biotransformation) can be estimated from
\[ {Cl}_{NR}= {Cl}_T- {Cl}_R\]
2) Kinetics of zero-order elimination: elimination rate is constant, t1/2 is dose-dependent (example: ethanol).
3)
\[ {C}_p= {C}_0- {k}_0t\]
- Multicompartment model
Non-instantaneous distribution from blood to tissue resulting in multiexponential plasma concentration curve, initial phase reflects distribution out of central compartment into total Vd, terminal phase reflects elimination.
\[ {C}_p=Ae^{-\alpha t}+Be^{-\beta t}\]
Where α and β are hybrid rate constants describing the 2 slopes.
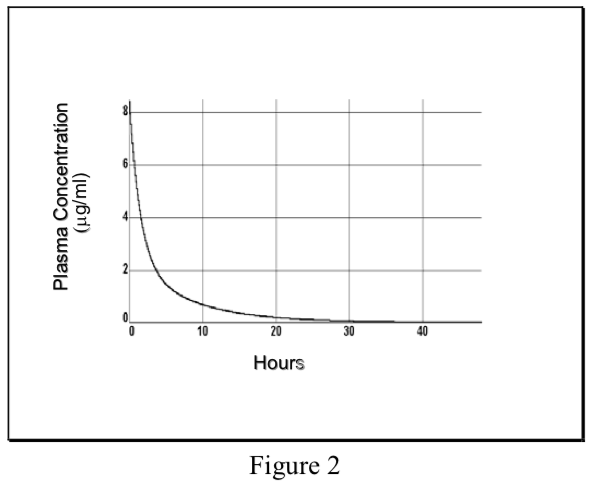
- Single compartment model
- Case with Non-Instantaneous Absorption
- Kinetics of first-order absorption and elimination: determination of absorption and elimination half-lives
\[ {C}_p={ {k}_aFD\over {V}_d( {k}_a- {k}_{el})}[{e^{- {k}_{el}t}-e^{- {k}_at}}]\]
Note that the terminal slope may be either the elimination rate constant, the absorption rate constant, or a hybrid
See Katzung, Basic & Clinical Pharmacology, 2001, p. 42
- Peak plasma concentration is dependent on absorption and elimination half-lives, volume of distribution, dose (D), and fraction of dose absorbed (F)
- \[AUC={F\cdot D\over {Cl}_T}\]
Fraction of dose absorbed into systemic circulation (F ) is the bioavailability of the drug product; determined experimentally by measuring AUC of dosage form of drug given by one route and comparing it to AUC of same dose of drug under conditions of complete absorption, i.e. given i.v.
- Kinetics of first-order absorption and elimination: determination of absorption and elimination half-lives
- Case with Highly Rapid Absorption Relative to Elimination
- Effect of infusions or multiple dosing on time-course of plasma concentrations
- Infusion Kinetics
One approach to maintaining a desired therapeutic level of a drug is to administer the agent by intravenous infusion. Drug delivery may be controlled by gravity- regulated drip of the agent into i.v. tubing or by use of an infusion pump.
- When a drug is administered at a constant dosing rate (DR) and its elimination follows first-order kinetics, the concentration of drug in the plasma rises exponentially and reaches a steady-state or plateau level (Css).
\[ {C}_p(t)= {C}_{ss}(1-e^{ {-k}_{el}t})\]
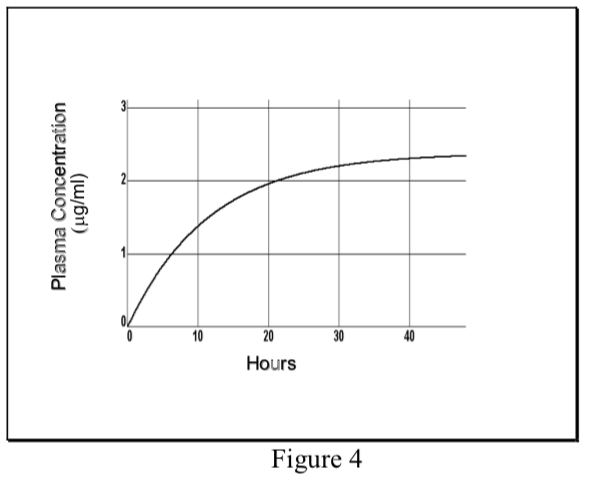
- At steady-state the INPUT RATE = OUTPUT RATE. The input rate is DR, which may be expressed as the total dose (D) divided by the length of the infusion (T). The output rate in the case of first-order elimination is the total amount of drug in the body (Css Vd) times the elimination rate constant (kel).
\[DR= {C}_{ss}\cdot {V}_d\cdot{k}_{el}\]
Therefore, the plasma concentration at steady-state can be predicted as follows:
\[ {C}_{ss}=DR\over {V}_d {k}_{el}\]
Remember that total clearance equals the elimination rate constant (kel) times the volume of distribution. Therefore, the plasma concentration at steady-state (Css) is directly proportional to the input rate (DR) of the drug and inversely proportional to its total plasma clearance (ClT).
\[ {C}_{ss}={DR\over {Cl}_T}\]
- The rate of achieving steady-state is dependent only on the elimination half-life of the drug. Half the Css level is achieved in one t1/2, and about 94% of Css in four t1/2.
- Because of the lag in achieving steady-state when a constant infusion rate is administered, a loading dose may be given to achieve the desired therapeutic effect more quickly. The loading dose may be chosen to produce the amount of drug in the body that would eventually be reached by the infusion alone.
\[Loading\ dose= {C}_{ss}\cdot {V}_d\]
At least on a theoretical basis, the plasma concentration will instantaneously reach the therapeutic level and that level will be maintained. Note that the steady-state level achieved with a continuous infusion is determined by the infusion rate and is not affected by the size of the loading dose.
- When a drug is administered at a constant dosing rate (DR) and its elimination follows first-order kinetics, the concentration of drug in the plasma rises exponentially and reaches a steady-state or plateau level (Css).
- Multiple Dosing Kinetics
- Commonly, drugs are administered repeatedly in order to maintain their therapeutic effects. In the simplest case, a maintenance dose (D) is given at a constant dosing interval (\(\tau\)) – [note that this is not the same as the time constant, \(\tau\)]. Since the route of administration may not be i.v., the amount of drug which reaches the systemic circulation may be some fraction (F) of the dose. If elimination is by first-order kinetics, a steady-state is eventually reached. The “average” Css at steady-state equals the fraction absorbed times dosing rate divided by total clearance, analogous to the Css from an infusion (see above).
\[ {C}_ss\ average={({F\cdot D\over\tau})\over {Cl}_T}$
- However, in the case of repetitive dosing, unlike an infusion, plasma concentrations of drug fluctuate during the dosing interval, depending on the kinetics of absorption and elimination. The degree of fluctuation in the plasma concentration during a dosing interval increases with increasing dose, dosing interval, clearance, and absorption rate.
- If a drug is administered i.v. (or where absorption is rapid and complete), the peak plasma concentration at steady-state (Cmaxss) relative to the peak after
the first dose (C0) depends on the ratio of the elimination half-life and the dosing interval (t1/2/\(\tau\)).
- \[ {C}_{ {mass}_{ss}}={ {C}_0\over1-f}\]
f is the fraction of drug remaining at the end of a dosing interval.
\[f=e^{ {-k}_{el}\cdot\tau}=e^{({-0.693\over {t}_{t/2}})\cdot\tau}=0.5^{\tau\over {t}_{1/2}}\]
Each time that the maintenance dose D is administered, the plasma concentration increases from Cmin to Cmax.. The decline from Cmax to Cmin is governed by the t1/2, just as in single dosing. These relationships are described mathematically as:
\[ {C}_{ {min}_{ss}}+{D\over {V}_d}= {C}_{ {max}_{ss}}\]
\[{D\over {V}_d}={C}_0\]
\[ {C}_{ {min}_{ss}}+ {C}_0= {C}_{ {max}_{ss}}\]
\[ {lnC}_{ {min}_{ss}}= {lnC}_{ {max}_{ss}}-({0.693\over {t}_{t/2}}\tau)\]
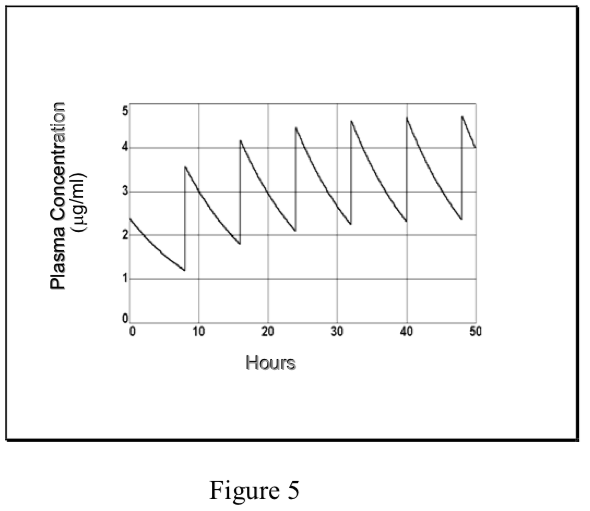
- Prediction of Cmax and Cmin at steady-state can be of great importance in cases where therapeutic efficacy is to be maintained while minimizing the risk of toxic side effects. (Note that the Css “average” described above lies between Cmaxss and Cminss, but it is not mathematically equivalent to their arithmetic or geometric mean.) The therapeutic window in a dosing regimen is the range of efficacious, non-toxic plasma concentrations lying between Cmaxss and Cminss. If these are known, then the dosing regimen is determined as follows:
\[Maintenance\ Dose = ( {C}_{ {max}_{ss}}- {C}_{ {min}_{ss}})\cdot {V}_d\]
\[Dosing \ interval \ (\tau)=[ln{ {C}_{ {max}_{ss}}\over {C}_{ {min}_{ss}}}][{ {t}_{t/2}\over0.693}]\]
- The rate of achieving steady-state is determined by the elimination half-life (as with an infusion). A loading dose may be used to rapidly achieve steady-state concentrations; especially important for drugs with long half-lives since attainment of steady-state is slow.
\[Loading\ dose = {C}_{ {max}_{ss}}\cdot {V}_d\]
- Commonly, drugs are administered repeatedly in order to maintain their therapeutic effects. In the simplest case, a maintenance dose (D) is given at a constant dosing interval (\(\tau\)) – [note that this is not the same as the time constant, \(\tau\)]. Since the route of administration may not be i.v., the amount of drug which reaches the systemic circulation may be some fraction (F) of the dose. If elimination is by first-order kinetics, a steady-state is eventually reached. The “average” Css at steady-state equals the fraction absorbed times dosing rate divided by total clearance, analogous to the Css from an infusion (see above).
- Infusion Kinetics
Time-Course of Drug Effect
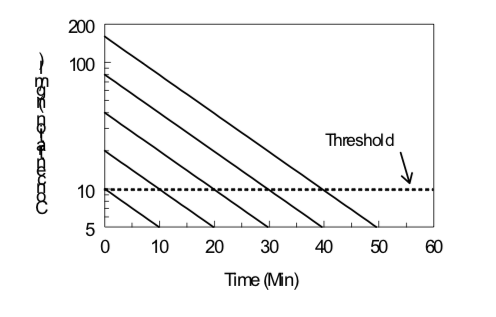
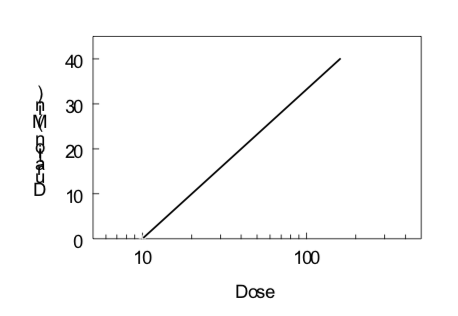
Under certain conditions (first-order kinetics, reversible effect, single compartment kinetics, iv administration), the elimination half-life of a drug and its threshold dose for a particular effect can be estimated by monitoring the effect of the drug as a function of time after drug administration. Data obtained from several doses can then be evaluated by examining the duration of a given level of effect as a function of the logarithm of the dose, as illustrated below. The slope is directly proportional to the elimination half-life; the steeper the slope (i.e., increase in duration with an increase in dose), the longer the elimination half-life. The x-intercept indicates the log of the threshold dose; the smaller the x-intercept the greater the potency of the drug.
\[Duration\ of\ Action ={ {t}_{1/2}\over0.301}(Log\ Dose\ - Log\ Threshold\ Dose)\]